Изгиб
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ИЗА |
| ИЗБ |
| ИЗВ |
| ИЗГ |
| ИЗД |
| ИЗЕ |
| ИЗЖ |
| ИЗИ |
| ИЗЛ |
| ИЗМ |
| ИЗН |
| ИЗО |
| ИЗР |
| ИЗУ |
| ИЗЪ |
| ИЗЮ |
| ИЗЯ |
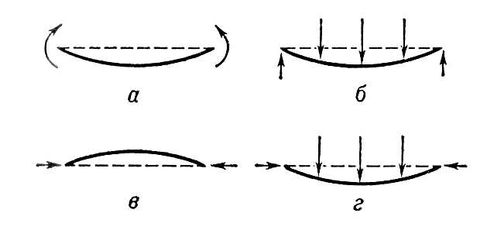
Изгиб в сопротивлении материалов, вид деформации, характеризующийся искривлением (изменением кривизны) оси или срединной поверхности деформируемого объекта (бруса, балки, плиты, оболочки и др.) под действием внешних сил или температуры. Применительно к прямому брусу различают Изгиб: простой, или плоский, при котором внешние силы лежат в одной из главных плоскостей бруса (т. е. плоскостей, проходящих через его ось и главные оси инерции поперечного сечения) (см. Моменты инерции); сложный, вызываемый силами, расположенными в разных плоскостях; косой, являющийся частным случаем сложного Изгиб (см. Косой изгиб). В зависимости от действующих в поперечном сечении бруса силовых факторов (рис. 1, а, б) Изгиб называется чистым (при наличии только изгибающих моментов) и поперечным (при наличии также и поперечных сил). В инженерной практике рассматривается также особый случай Изгиб — продольный Изгиб (рис. 1, в), характеризующийся выпучиванием стержня под действием продольных сжимающих сил (см. Продольный изгиб). Одновременное действие сил, направленных по оси стержня и перпендикулярно к ней, вызывает продольно-поперечный Изгиб (рис. 1, г).
Рис. 1. Изгиб бруса: а — чистый: б — поперечный; в — продольный; г — продольно-поперечный.
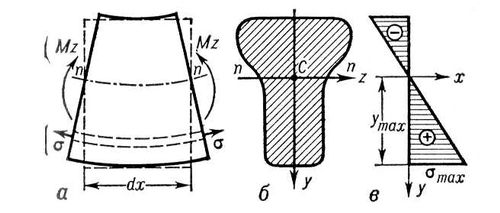
Приближённый расчёт прямого бруса на действие Изгиб в упругой стадии производится в предположении, что поперечные сечения бруса, плоские до Изгиб, остаются плоскими и после него (гипотеза плоских сечений); полагают также, что продольные волокна бруса при Изгиб не давят друг на друга и не стремятся оторваться одно от другого. При плоском Изгиб в поперечных сечениях бруса возникают нормальные и касательные напряжения. Нормальные напряжения s в произвольном волокне какого-либо поперечного сечения бруса (рис. 2), лежащем на расстоянии y от нейтральной оси, определяются формулой 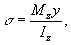 где Mz— изгибающий момент в сечении, a Iz — момент инерции поперечного сечения относительно нейтральной оси. Наибольшие нормальные напряжения возникают в крайних волокнах сечения
где Mz— изгибающий момент в сечении, a Iz — момент инерции поперечного сечения относительно нейтральной оси. Наибольшие нормальные напряжения возникают в крайних волокнах сечения 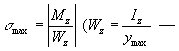 момент сопротивления поперечного сечения). Касательные напряжения t, возникающие при поперечном Изгиб, определяются по формуле Д. Изгиб Журавского
момент сопротивления поперечного сечения). Касательные напряжения t, возникающие при поперечном Изгиб, определяются по формуле Д. Изгиб Журавского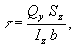 где Qy — поперечная сила в сечении, Sz — статический момент относительно нейтральной оси части площади поперечного сечения, расположенной выше (или ниже) рассматриваемого волокна, b— ширина сечения на уровне рассматриваемого волокна. Характер изменения изгибающих моментов и поперечных сил по длине бруса обычно изображается графиками-эпюрами, по которым определяются их расчётные значения. Под влиянием Изгиб ось бруса искривляется, ее кривизна определяется выражением
где Qy — поперечная сила в сечении, Sz — статический момент относительно нейтральной оси части площади поперечного сечения, расположенной выше (или ниже) рассматриваемого волокна, b— ширина сечения на уровне рассматриваемого волокна. Характер изменения изгибающих моментов и поперечных сил по длине бруса обычно изображается графиками-эпюрами, по которым определяются их расчётные значения. Под влиянием Изгиб ось бруса искривляется, ее кривизна определяется выражением 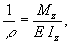 где r — радиус кривизны оси изогнутого бруса в рассматриваемом сечении; Е — модуль продольной упругости материала бруса. В случаях малых деформаций кривизна приближённо выражается второй производной от прогиба V, а поэтому между координатами изогнутой оси и изгибающим моментом существует дифференциальная зависимость
где r — радиус кривизны оси изогнутого бруса в рассматриваемом сечении; Е — модуль продольной упругости материала бруса. В случаях малых деформаций кривизна приближённо выражается второй производной от прогиба V, а поэтому между координатами изогнутой оси и изгибающим моментом существует дифференциальная зависимость 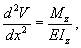 называемая дифференциальным уравнением оси изогнутого бруса. Решением этого уравнения определяется упругая линия балки (бруса).
называемая дифференциальным уравнением оси изогнутого бруса. Решением этого уравнения определяется упругая линия балки (бруса).
Рис. 2. Чистый изгиб прямого бруса в упругой стадии: а — элемент бруса; б — поперечное сечение; в — эпюра нормальных напряжений.
Расчёт бруса на Изгиб с учётом пластических деформаций приближённо производится в предположении, что при возрастании нагрузки (изгибающего момента) первоначально в крайних точках (волокнах), а затем и во всём поперечном сечении возникают пластические деформации. Распределение напряжений в предельном состоянии имеет вид двух прямоугольников с ординатами, равными пределу текучести материала sт, при этом кривизна бруса неограниченно возрастает. Такое состояние в сечении называется пластическим шарниром, а соответствующий ему момент является предельным и определяется по формуле 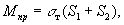 в которой S1 и S2 — статические моменты сжатой и растянутой частей сечения относительно нейтральной оси.
в которой S1 и S2 — статические моменты сжатой и растянутой частей сечения относительно нейтральной оси.
Лит. см. при ст. Сопротивление материалов.
Л. В. Касабьян.
|
Так же Вы можете узнать о... Костный мозг, ткань, заполняющая полости костей у позвоночных животных и человека. Кроветворные органы, Органы животных и человека, в которых образуются форменные элементы крови и лимфы. Куртина (франц. courtine), 1) в регулярном парке — открытый участок газона, обрамленный стрижеными кустами или деревьями; в пейзажном парке — свободно стоящая группа деревьев, кустов (см. Лача, Лаче, озеро в истоках р. Онеги, в Архангельской области РСФСР. Лизергиновая кислота, органическая кислота сложного строения, C16H16O2N2, содержащая остаток индола. Луанда (Loanda), город, административный центр Анголы. Макапагал Фелисисимо (р. 5.12.1914, Сан-Хулиано, провинция Нуэва-Эсиха), деятель коммунистического движения на Филиппинах. Мартынов Андрей Васильевич [9(21).8.1879, Рязань,—29. Меланоцитостимулирующий гормон, МСГ, меланотропин, интермедин, гормон животных и человека, выделяемый задней и промежуточноaй долями гипофиза, участвует в образовании пигментов покровов и сетчатки глаза. Миллес Карл Миллес (Milles) Карл (23.6.1875, Лагга, близ Упсалы, — 19. Монастырский приказ, один из органов центрального правительственного управления в Русском государстве, осуществлявший контроль над церковными вотчинами. |
|