Остаточный член
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ОСА |
| ОСБ |
| ОСВ |
| ОСЕ |
| ОСЁ |
| ОСИ |
| ОСК |
| ОСЛ |
| ОСМ |
| ОСН |
| ОСО |
| ОСП |
| ОСС |
| ОСТ |
| ОСУ |
| ОСФ |
| ОСЦ |
| ОСЫ |
| ОСЬ |
| ОСЯ |
Остаточный член приближённой формулы, разность между точным и приближённым значениями представляемого этой формулой выражения. В зависимости от характера приближённой формулы Остаточный член может иметь различный вид. Обычно задача исследования Остаточный член состоит в том, чтобы получить для него оценки. Например, приближённой формуле 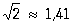
соответствует точное равенство 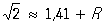 ,
,
где выражение R является Остаточный член для приближения 1,41 к числу 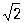 и известно, что 0,004 < R < 0,005. Далее, Остаточный член постоянно встречается в асимптотических формулах. Например, для числа p(х) простых чисел, не превосходящих х, имеем асимптотическую формулу
и известно, что 0,004 < R < 0,005. Далее, Остаточный член постоянно встречается в асимптотических формулах. Например, для числа p(х) простых чисел, не превосходящих х, имеем асимптотическую формулу 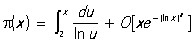 ,
,
где m — любое положительное число, меньшее 3/5; здесь Остаточный член, являющийся разностью
между функциями p(х) и 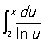 для х ³ 2, записан в виде
для х ³ 2, записан в виде 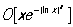 , где буква О обозначает, что Остаточный член не превосходит по абсолютной величине выражения
, где буква О обозначает, что Остаточный член не превосходит по абсолютной величине выражения 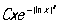 , а С — некоторая положительная постоянная. Можно говорить об Остаточный член формулы, дающей приближённое представление функции. Например, в Тейлора формуле
, а С — некоторая положительная постоянная. Можно говорить об Остаточный член формулы, дающей приближённое представление функции. Например, в Тейлора формуле 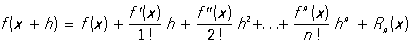
Остаточный член Rn (x) в форме Лагранжа имеет вид 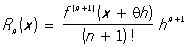 ,
,
где q — некоторое число, причём 0 < q < 1 (q зависит, вообще говоря, от выбранных значений х и h). Наличие в формуле для Rn (x) числа q вносит некоторую неопределённость; такого рода неопределённость свойственна многим формулам для Остаточный член
Можно говорить об Остаточный член квадратурной формулы, интерполяционных формул и т.д.
|
Так же Вы можете узнать о... Аренга (Arenga), род высоких (до 15 м) стройных пальм с широкой кроной крупных перистых тёмно-зелёных (снизу серебристых) листьев. Бар (город в Югославии) Бар (Bar), город и порт в Югославии, в Черногории, на побережье Адриатического моря. Бланкизм, политическое течение, связанное с именем Л. Бухта (нем. Bucht), небольшая часть моря, залива, озера, водохранилища, обособленная от открытых вод частями суши. Вилкавишкис, город, центр Вилкавишкского района Литовской ССР. Вьенна (река во Франции) Вьенна (Vienne), река на З. Франции, левый приток Луары. Гидролизная промышленность, объединяет производства, основанные на химической переработке растительных материалов путём каталитического превращения полисахаридов в моносахариды. Грицевец Сергей Иванович (6.7.1909—16.9.1939), лётчик, дважды Герой Советского Союза (22. Джаландхар, Джалландар, город в северо-западной Индии, в штате Пенджаб, в междуречье Биас—Сатледж, на важном историческом пути в Индию из Малой и Средней Азии. Дьяченко Василий Петрович [28.7(10.8).1902, Кустанай, — 23. Земной магнетизм, геомагнетизм, магнитное поле Земли и околоземного космического пространства; раздел геофизики, изучающий распределение в пространстве и изменения во времени геомагнитного поля, а также связанные с ним геофизические процессы в Земле и верхней атмосфере. Ионизирующие излучения, ионизующие излучения, излучения, взаимодействие которых со средой приводит, в конечном счёте, к ионизации атомов и молекул. |
|