Синусоидальные спирали
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| СИА |
| СИБ |
| СИВ |
| СИГ |
| СИД |
| СИЕ |
| СИЗ |
| СИИ |
| СИЙ |
| СИК |
| СИЛ |
| СИМ |
| СИН |
| СИО |
| СИП |
| СИР |
| СИС |
| СИТ |
| СИУ |
| СИФ |
| СИХ |
| СИЦ |
| СИШ |
| СИЭ |
Синусоидальные спирали, синус-спирали, кривые, уравнения которых в полярной системе координат имеют вид
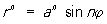 , (*)
, (*)
где n — рациональное число. Частными случаями Синусоидальные спирали являются окружность, прямая, равнобочная гипербола, лемниската, кардиоида, парабола (см. Линия)
(соответственно при n = 1, —1, —2, 2, 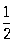 ,
, 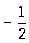 ). Логарифмическую спираль можно рассматривать как некоторый предельный случай Синусоидальные спирали при n = 0 [хотя уравнение (*) теряет при этом смысл], разделяющей Синусоидальные спирали, лежащие в конечной части плоскости, от Синусоидальные спирали, имеющих бесконечные ветви. Проекция центра кривизны любой точки Синусоидальные спирали на радиус-вектор этой точки делит его в отношении n: 1 (считая от полюса). При равномерном вращении радиус-вектора Синусоидальные спирали вокруг полюса касательная равномерно вращается вокруг точки касания. Поэтому Синусоидальные спирали называются также кривыми пропорционального изгиба. При натуральном n Синусоидальные спирали состоит из n лепестков, лежащих в углах
). Логарифмическую спираль можно рассматривать как некоторый предельный случай Синусоидальные спирали при n = 0 [хотя уравнение (*) теряет при этом смысл], разделяющей Синусоидальные спирали, лежащие в конечной части плоскости, от Синусоидальные спирали, имеющих бесконечные ветви. Проекция центра кривизны любой точки Синусоидальные спирали на радиус-вектор этой точки делит его в отношении n: 1 (считая от полюса). При равномерном вращении радиус-вектора Синусоидальные спирали вокруг полюса касательная равномерно вращается вокруг точки касания. Поэтому Синусоидальные спирали называются также кривыми пропорционального изгиба. При натуральном n Синусоидальные спирали состоит из n лепестков, лежащих в углах
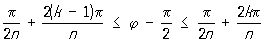 ,
, 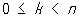
касаясь в начале координат сторон угла. Углы
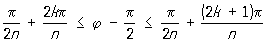 ,
, 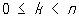
не содержат точек Синусоидальные спирали, отличных от начала координат. Если вписать в круг радиуса а.2-1/n правильный n-угольник P1, P2,..., Рп, то множество точек, произведение расстояний которых до точек P1, P2,..., Рп равно an/2, является Синусоидальные спирали Площадь одного лепестка Синусоидальные спирали равна
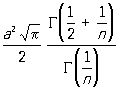 ,
,
а периметр равен
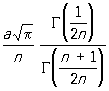
где G(х) — гамма-функция. При натуральном n Синусоидальные спирали имеет n осей симметрии. Если n = 1/q, то кривая симметрична относительно полярной оси, причём каждая из половин кривой имеет вид спирали, начинающейся в точке r = а,j = p/2 и после оборота на угол qp/2 приходящей в полюс. Синусоидальные спирали при n = p/q является алгебраической кривой (см. Алгебраическая геометрия), обладающей р осями симметрии, наклоненными к вертикальной оси под углами 2pqk/p, 0 £k < p. Изучение Синусоидальные спирали с отрицательными значениями п сводится к изучению Синусоидальные спирали с положительными п при помощи преобразования инверсии. Синусоидальные спирали применяются в некоторых вопросах механики, геодезии и др.
|
Так же Вы можете узнать о... Бессточные области, области с засушливым климатом, не имеющие в силу этого стока поверхностных вод ни во внутренние моря, ни в Мировой океан. Глазунов Александр Александрович [7(19).11.1891, Москва, — 5. Ингури, Ингур, река в Западной Грузии. Длина 213 км, площадь бассейна 4060 км2. Купоросы, техническое название кристаллогидратов сернокислых солей (сульфатов) некоторых тяжёлых металлов. Мэр (франц. maire, англ. mayor, от лат. major — больший, старший), высшее должностное лицо в муниципалитетах США, Великобритании, Франции и ряда др. Полярон, электрон, двигающийся по кристаллу вместе с вызываемой им деформацией решётки. Словакия (Slovensko), Словацкая Социалистическая Республика (ССР; Slovenska socialisticka republika), республика в составе Чехословакии (ЧССР). Фанг, пангве, пахуин, группа родственных народов (яунде, булу, бене, бети и др. Эфиры сложные, органические соединения, производные кислот, в молекулах которых гидроксильная группа OH замещена на остаток спирта, енола или фенола — OR, например C2H5OCOCH3, C5H11ONO. Бонин, Огасавара, вулканический архипелаг из 89 мелких островов в западной части Тихого океана. Гресли Аманц Гресли (Gressly) Аманц (17.7.1814, близ Лауфена, — 13. Кайлас, горный хребет в Китае, на Ю. Тибетского нагорья. Лесные полосы, искусственные защитные насаждения в форме узких лент, среди пахотных массивов, вдоль ж. Нитрилы карбоновых кислот, цианистые соединения, RC ≡ N, органические производные синильной кислоты. Публицистика (от лат. publicus — общественный), род произведений, посвященных актуальным вопросам и явлениям текущей жизни общества и содержащих фактические данные о различных её сторонах, оценки с точки зрения социального идеала автора, а также представления о путях и способах достижения выдвинутых целей. Стекловидное тело, 1) прозрачное бессосудистое студенистое вещество, заполняющее полость глаза между сетчаткой и хрусталиком. Хараппа, руины одного из главных центров хараппской цивилизации, расположены близ старого русла р. Акусма (греч. ákusma — услышанное), слуховое представление, участвующее, по мнению некоторых фонетистов, в образовании комплексного образа звука, например представление «носового характера» звуков «н» и «м» в русском языке, ср. |
|