Статистических решений теория
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
Утеплитель изорок изолайт купить utepliteli-77.ru. |
| СТА |
| СТВ |
| СТЕ |
| СТЁ |
| СТИ |
| СТЛ |
| СТО |
| СТР |
| СТУ |
| СТШ |
| СТЫ |
| СТЬ |
| СТЭ |
| СТЮ |
| СТЯ |
Статистических решений теория, часть математической статистики и игр теории, позволяющая единым образом охватить такие разнообразные задачи, как статистическая проверка гипотез, построение статистических оценок параметров и доверительных границ для них, планирование эксперимента и др. В основе Статистических решений теория лежит предположение, что распределение вероятностей F наблюдаемой случайной величины XF принадлежит некоторому априори данному множеству 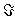 . Основная задача Статистических решений теория состоит в отыскании наилучшего статистического решения или решающего правила (функции) d = d (x), позволяющего по результатам наблюдений х над Х судить об истинном (но неизвестном) распределении F. Для сравнения достоинств различных решающих правил вводят в рассмотрение функцию потерь W [F, d (x)], представляющую убыток от принятия решения d (x) (из заданного множества D), когда истинное распределение есть F. Естественно было бы считать решающее правило d* = d*(x) наилучшим, если средний риск r (F, d*) =MFW [F, d (X)] (MF — усреднение по распределению F) не превышает r (F, d) для любого FÎ
. Основная задача Статистических решений теория состоит в отыскании наилучшего статистического решения или решающего правила (функции) d = d (x), позволяющего по результатам наблюдений х над Х судить об истинном (но неизвестном) распределении F. Для сравнения достоинств различных решающих правил вводят в рассмотрение функцию потерь W [F, d (x)], представляющую убыток от принятия решения d (x) (из заданного множества D), когда истинное распределение есть F. Естественно было бы считать решающее правило d* = d*(x) наилучшим, если средний риск r (F, d*) =MFW [F, d (X)] (MF — усреднение по распределению F) не превышает r (F, d) для любого FÎ 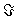 и любого решающего правила d = d (x). Однако такое «равномерно наилучшее» решающее правило в большинстве задач отсутствует, в связи с чем наибольший интерес в Статистических решений теория представляет отыскание т. н. минимаксных и бейесовских решений. Решение
и любого решающего правила d = d (x). Однако такое «равномерно наилучшее» решающее правило в большинстве задач отсутствует, в связи с чем наибольший интерес в Статистических решений теория представляет отыскание т. н. минимаксных и бейесовских решений. Решение 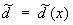 называется минимаксным, если
называется минимаксным, если
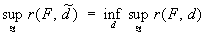
Решение 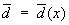 называется бейесовским (относительно заданного априорного распределения n на множестве
называется бейесовским (относительно заданного априорного распределения n на множестве 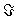 ), если для всех решающих правил d
), если для всех решающих правил d
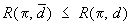 ,
,
где
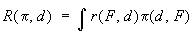
между минимаксными и бейесовскими решениями существует тесная связь, заключающаяся в том, что в весьма широких предположениях о данных задачи минимаксное решение является бейесовским относительно «наименее благоприятного» априорного распределения p.
Лит.: Вальд А., Статистические решающие функции, в сборнике: Позиционные игры, М., 1967: Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964.
А. Н. Ширяев.
|
Так же Вы можете узнать о... Простирание и падение (геологические), характеристики положения (элементы залегания) слоя горных пород, кровли магматического массива, жилы и др. Руданский Степан Васильевич [25.12.1833 (6.1. Синуиты, синуситы (от лат. sinus — изгиб, пазуха), воспаление придаточных пазух носа человека и животных. Стронгилятозы лошадей, болезни преимущественно лошадей, а также ослов и мулов, вызываемые круглыми червями стронгилятами, паразитирующими в кишечнике. Торричелли Эванджелиста Торричелли (Torricelli) Эванджелиста (15.10. Фиджийский язык, фиджи язык, язык фиджийцев, коренного населения островов Фиджи. Центральная Африка, Экваториальная Африка, природная страна, охватывающая западную часть Африки в экваториальных и субэкваториальных широтах, между Гвинейским заливом и Атлантическим океаном на З. Щоголев Яков Иванович [24.10(5.11).1823, г. Ахтырка, ныне Сумской обл. Аганбегян Абел Гезевич (р. 8.10.1932, Тбилиси), советский экономист, член-корреспондент АН СССР (1964). Асатиани Георгий Ираклиевич [р. 28.5(10.6).1914, г. Бироновщина, крайне реакционный режим в России в 30-х гг. Венесуэльский кризис 1902-03 Венесуэльский кризис 1902—03, международный кризис, явившийся следствием обострения империалистических противоречий в бассейне Карибского моря. Гаошань (кит. — горцы), собирательное название группы племён, живущих в КНР на островах Тайвань [племена атайял, цоу, амэй (ами), бунун, паиван, сайсет] и Хунтоуюй [племя емэй (ями)]. Гроссето (Grosseto), город в Италии, в обл. Тоскана. Драгович Радован Драгович (Драговић) Радован (10.12.1878, Ужице, — 7. Идюм, река в Хабаровском крае РСФСР и по границе его с Якутской АССР, правый приток р. Карлайл (Carlisle), город-графство в Великобритании, на р. Кондратьев Виктор Николаевич [р. 19.1(1.2).1902, Рыбинск], советский физико-химик, академик АН СССР (1953; член-корреспондент 1943). |
|