Грина формулы

Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я 1 2 3 4 8 A L M P S T X
ГА ГБ ГВ ГД ГЕ ГЁ ГЖ ГЗ ГИ ГЛ ГМ ГН ГО ГП ГР ГС ГУ ГХ ГЫ ГЬ ГЭ ГЮ ГЯ
ГРА
ГРЕ
ГРЁ
ГРЖ
ГРИ
ГРО
ГРУ
ГРЫ
ГРЭ
ГРЮ
ГРЯ

Грина формулы, формулы интегрального исчисления, связывающие между собой интегралы различных типов. Простейшая из них связывает двойной интеграл по области G с криволинейным интегралом по границе С области G и имеет вид: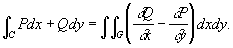

Эта формула была известна ещё Л. Эйлеру (1771). Две другие впервые опубликованы Джорджем Грином в 1828 в связи с исследованиями по теории потенциала: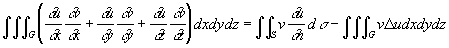

(первая Грина формулы, или предварительная Грина формулы) и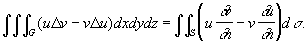

Здесь G — область трёхмерного пространства, поверхность S — граница этой области, Du = 2u/x2 + 2u/y2 + 2u/z2 (аналогично Dv) — оператор Лапласа, u/n, v/n — производные по направлению внешней нормали к S.

 
Так же Вы можете узнать о...


Импульсные источники света, предназначаются для получения одиночных или периодически повторяющихся световых вспышек длительностью от долей мксек до нескольких десятков мсек.
Исполнение музыкальное, воспроизведение музыки с помощью тех или иных исполнительских средств, вид художественного творчества.
Калькуляция (лат. calculatio, от calculo — считаю, подсчитываю), исчисление себестоимости единицы продукции или выполненной работы.
Карло-Либкнехтовск, город (с 1965) в Донецкой области Украинской ССР, в 18 км от Артёмовска, в 2 км от ж.
Кемпбелл Дуглас Хоутон Кемпбелл (Campbell) Дуглас Хоутон (1859—1953), американский ботаник; см.
Клермон-Ферран (Clermont-Ferrand), город во Франции, в долине р.
Колюр солнцестояний, большой круг небесной сферы, проходящий через полюсы мира и точки летнего и зимнего солнцестояния.
Копель, медно-никелевый сплав, содержащий ~43% Ni и ~0,5% Mn.
Крапивница (аллергич. р-ция организма) Крапивница, уртикария (от лат. urtica — крапива), аллергическая реакция организма, характеризующаяся внезапным и быстрым появлением на коже (иногда и слизистой гортани) волдырей, сопровождающихся сильным зудом.
Кубанит (от исп. cubano — кубинский, по месторождению на о.