Максвелла распределение
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| МАА |
| МАБ |
| МАВ |
| МАГ |
| МАД |
| МАЕ |
| МАЁ |
| МАЖ |
| МАЗ |
| МАИ |
| МАЙ |
| МАК |
| МАЛ |
| МАМ |
| МАН |
| МАО |
| МАП |
| МАР |
| МАС |
| МАТ |
| МАУ |
| МАФ |
| МАХ |
| МАЦ |
| МАЧ |
| МАШ |
| МАЭ |
| МАЮ |
| МАЯ |
Максвелла распределение, распределение по скоростям (или импульсам) молекул системы, находящейся в состоянии термодинамического равновесия. Впервые установлено Дж. К. Максвеллом в 1859. Согласно Максвелла распределение, вероятность Dw (vx, vy, vz) того, что проекции скорости молекулы лежат в малых интервалах от vx до vx+ Dvx, от vy до vy+ Dvy и от vz до vz+ Dvz определяется формулой: 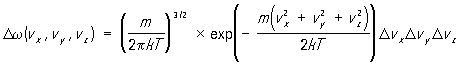 (1)
(1)
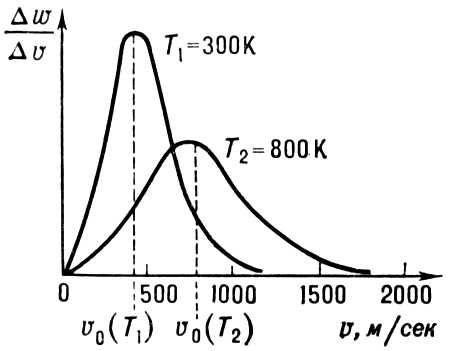
Распределение молекул азота по скоростям v при двух значениях абсолютной температуры T1 и T2; Dw/Dv — отношение вероятности того, что абсолютное значение скорости лежит в интервале от v до v + Dv к интервалу скорости Dv.
Здесь m — масса молекулы, Т — абсолютная температура системы, k — постоянная Больцмана.
Вероятность того, что абсолютное значение скорости лежит в интервале от v до v+ Dv, вытекает из (1) и имеет вид:
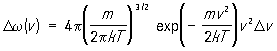 (2)
(2)
Эта вероятность достигает максимума при
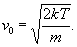
Скорость v0 называется наиболее вероятной. Чем ниже температура системы, тем большее число молекул имеют скорости, близкие к наиболее вероятной (см. рисунок).
Среднее число частиц в 1 см3 газа со скоростями в интервале от v до v+ Dv равно Dn(v) = n0Dw(v), где n0 — полное число частиц в 1 см3.
С помощью Максвелла распределение можно вычислять средние значения скоростей молекул и любых функций этих скоростей. В частности, средняя квадратичная скорость 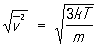
лишь немного (в 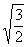 раз) превышает наиболее вероятную скорость. Например, для азота при Т » 300 К
раз) превышает наиболее вероятную скорость. Например, для азота при Т » 300 К 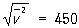 м/сек, a v0 » 360 м/сек.
м/сек, a v0 » 360 м/сек.
Максвелла распределение вытекает из Гиббса распределения канонического в том случае, когда поступательное движение частиц можно рассматривать в классическом приближении (см. Статистическая физика). Максвелла распределение не зависит от характера взаимодействия частиц системы и от внешних сил и потому справедливо как для молекул газа, так и для молекул жидкостей и твёрдых тел. Максвелла распределение справедливо также для броуновских частиц, взвешенных в газе или жидкости (см. Броуновское движение).
Экспериментальное подтверждение Максвелла распределение получено в опытах с молекулярными пучками.
Лит.: Кикоин И. К., Кикоин А. К., Молекулярная физика, М., 1963; Штрауф Е. А., Молекулярная физика, Л. — М., 1949.
Г. Я. Мякишев.
|
Так же Вы можете узнать о... Вибрационная болезнь, профессиональное заболевание, вызванное длительным воздействием на организм местной (локальной) или общей вибрации. Выводковые почки, 1) у покрытосеменных растений почки, которые могут отрываться от материнского организма и, прорастая, давать новые растения; во многих случаях В. Гетеро... (от греч. héteros — иной, другой), составная часть сложных слов, означающая разнородность, чужеродность (противоположное гомо. Графито-газовый реактор, ядерный реактор на тепловых нейтронах, в котором замедлителем служит графит, а теплоносителем — газ, обычно двуокись углерода, реже — гелий. Дербышев Николай Иванович (9(21).3.1879, Томск, — 13. Дуадастанон, осетинский музыкальный инструмент типа арфы. Затинщики, в Русском государстве 16—17 вв. категория служилых людей, обслуживавших «затинную» (стоявшую за крепостной стеной) артиллерию. Инженерно-авиационная служба, одна из служб в военно-воздушных силах СССР. Канадский рис (Zizania aquatica), злак из рода зизания, дико растущий в Северной Америке. Кикимора, шишимора, мара, в русских народных поверьях — малютка-невидимка женского пола (голова с напёрсток, туловище тонкое, как соломинка), живущая в доме за печкой и занятая прядением и тканьём. Комуз, 1) киргизский струнный щипковый музыкальный инструмент. Крживицкий Людвиг Крживицкий (Krzywicki) Людвиг (1859—1941), польский учёный и публицист; см. |
|