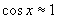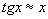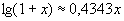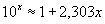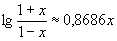Приближённое решение
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПРА |
| ПРЕ |
| ПРЁ |
| ПРЖ |
| ПРИ |
| ПРО |
| ПРУ |
| ПРШ |
| ПРЫ |
| ПРЮ |
| ПРЯ |
Приближённое решение дифференциальных уравнений, получение аналитических выражений (формул) или численных значений, приближающих с той или иной степенью точности искомое частное решение дифференциального уравнения.
Приближённое решение дифференциальных уравнений в виде аналитического выражения может быть найдено методом рядов (степенных, тригонометрических и др.), методом малого параметра, последовательных приближений методом, Ритца и Галёркина методами, Чаплыгина методом. Каждый из этих методов определяет один или несколько бесконечных процессов, с помощью которых при выполнении определённых условий можно получить точное решение задачи. Для получения Приближённое решение останавливаются на некотором шаге процесса.
Если решение ищется в виде бесконечного ряда, то за Приближённое решение принимают конечный отрезок ряда. Например, пусть требуется найти решение дифференциального уравнения y' = f (x, у), удовлетворяющее начальным условиям у (х0) = y0, причём известно, что f (x, у) — аналитическая функция х, у в некоторой окрестности точки (х0, y0). Тогда решение можно искать в виде степенного ряда: y (x) y (x0) =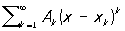 .
.
Коэффициенты Ak ряда могут быть найдены либо по формулам: A1= y’0= f (x0, y0); 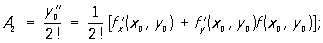
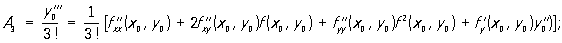
либо с помощью неопределенных коэффициентов метода. Метод рядов позволяет находить решение лишь при малых значениях величины х — х0.
Часто (например, при изучении периодических движений в небесной механике и теории колебаний) встречается случай, когда уравнение состоит из членов двоякого вида: главных и второстепенных, причём второстепенные члены характеризуются наличием в них малых постоянных множителей. Обычно после отбрасывания второстепенных членов получается уравнение, допускающее точное решение. Тогда решение основного уравнения можно искать в виде ряда, первым членом которого является решение уравнения без второстепенных членов, а остальные члены ряда расположены по степеням малых постоянных величин, входящих во второстепенные члены (малых параметров). При этом уравнения для коэффициентов при степенях малых параметров линейны, что облегчает их решение. В роли малого параметра иногда выступают начальные значения (например, при изучении колебаний около положения равновесия). Метод малого параметра был использован при решении задачи о возмущённом движении в небесной механике Л. Эйлером и П. Лапласом. Теоретическое обоснование этого метода дали А. М. Ляпунов и А. Пуанкаре.
К численным методам относятся методы, позволяющие находить Приближённое решение при некоторых значениях аргумента (т. е. получать таблицу приближённых значений искомого решения), пользуясь известными значениями решения в одной или нескольких точках. Такими методами являются, например, метод Эйлера, метод Рунге и целый ряд разностных методов.
Поясним эти методы на примере уравнения y’’ = f (x, у)
с начальным условием у (х0) = y0. Пусть точное решение этого уравнения представлено в некоторой окрестности точки х0 в виде ряда по степеням h = х — х0 Основной характеристикой точности формул Приближённое решение дифференциальных уравнений является требование, чтобы первые k членов разложения в ряд по степеням h Приближённое решение совпадали с первыми k членами разложения в ряд по степеням h точного решения.
Основная идея метода Эйлера заключается в применении метода рядов для вычисления приближённых значений решения у (х) в точках x1, x2,..., xn некоторого фиксированного отрезка [х0, b] Так, для того чтобы вычислить у (х1), где х1 = х0 + h, h = (b — x0)/n, представляют у (х1) в виде конечного числа членов ряда по степеням h = х1— х0. Например, ограничиваясь первыми двумя членами ряда, получают для вычисления у (xk) формулы: 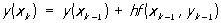 ,
, 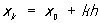
Это т. н. метод ломаных Эйлера (на каждом отрезке [xk, xk+1] интегральная кривая заменяется прямолинейным отрезком — звеном ломаной Эйлера). Погрешность метода пропорциональна h2.
В методе Рунге вместо того, чтобы отыскивать производные, находят такую комбинацию значений f (x, у) в некоторых точках, которая даёт с определённой точностью несколько первых членов степенного ряда для точного решения уравнения. Например, правая часть формулы Рунге: 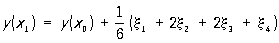 ,
,
где 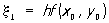 ;
; 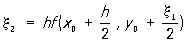 ;
; 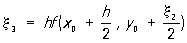 ;
; 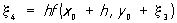
дает первые пять членов степенного ряда с точностью до величин порядка h5.
В разностных формулах Приближённое решение удаётся несколько раз использовать уже вычисленные значения правой части. Решение ищется в виде линейной комбинации у (xi), hi и разностей Dihj, где hj = hf (xj, yj); Dhj = hj+1 hj; Dihj = Di-1hj+1 Di-1hj.
Примером разностной формулы Приближённое решение является экстраполяционная формула Адамса. Так, формула Адамса, учитывающая «разности» 3-го порядка: 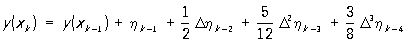
даёт решение у (х) в точке xk с точностью до величин порядка h4.
Для уравнений 2-го порядка можно получить формулы численного интегрирования путём двукратного применения
|
Формула |
k = 2 |
k = 3 |
k = 4 |
|
(1 + x)3» 1 + 3x |
0,04 |
0,012 |
0,004 |
|
|
0,06 |
0,022 |
0,007 |
|
|
0,19 |
0,062 |
0,020 |
|
|
0,20 |
0,065 |
0,021 |
|
|
0,31 (17°48') |
0,144 (8°15') |
0,067 (3°50') |
|
|
0,10 (5°43') |
0,031 (l'48') |
0,010 (0°34') |
|
|
0,25 (14°8') |
0,112 (6°25') |
0,053 (3°2') |
|
|
0,14 |
0,47 |
0,015 |
|
|
0,04 |
0,014 |
0,004 |
|
|
0,25 |
0,119 |
0,055 |
формулы Адамса. Норвежский математик К. Стёрмер получил формулу: 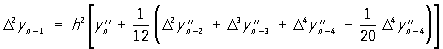
особенно удобную для решения уравнений вида у'' = f (x, у). По этой формуле находят D2yn-1, а затем yn+1 = yn +Dyn+1 + D2yn-1. Найдя yn+1, вычисляют y’’n+1= f (xn+1,yn+1), находят разности и повторяют процесс далее.
Указанные выше численные методы распространяются и на системы дифференциальных уравнений.
Значение численных методов решения дифференциальных уравнений особенно возросло с распространением ЭВМ.
Кроме аналитических и численных методов, для Приближённое решение дифференциальных уравнений применяются графические методы. В простейшем из них строят поле направлений, определяемое дифференциальным уравнением, т. е. в некоторых точках рисуют направления касательной к интегральной кривой, проходящей через эту точку. Затем проводят кривую так, чтобы касательные к ней имели направления поля (см. Графические вычисления).
Лит.: Березин И. С., Жидков Н. П., Методы вычислений, 2 изд., т. 2, М.. 1962; Бахвалов Н. С., Численные методы, М., 1973: Коллатц Л., Численные методы решения дифференциальных уравнений, пер. с нем., М., 1953; Милн В. Э., Численное решение дифференциальных уравнений, пер, с англ., М., 1955.
|
Так же Вы можете узнать о... Бактерицидность (от бактерии и лат. caedo — убиваю), способность физических, химических и биологических факторов убивать микроорганизмы. Беллоу Сол Беллоу (Bellow) Сол (p. 10.7.1915, Лашин, Квебек), американский писатель. Блатенское княжество, раннефеодальное славянское государство, существовавшее в 9 в. Бретонская лошадь, тяжеловозная лошадь, выведенная в северо-западных районах Франции (Бретань) скрещиванием местных упряжных лошадей с першеронами и норфольками. Валаамова ослица, согласно древнееврейскому мифу (сохранённому в библейской книге Чисел), ослица прорицателя Валаама, на которой он ехал к царю государства Моав Валаку, чтобы проклясть израильтян, ведших войну с Моавом, и обеспечить моавитянам победу. Вес 1000 семян, один из важных показателей качества семенного материала. Военное издательство Министерства обороны СССР, издаёт военно-научную, военно-техническую, военно-политическую и художественную литературу для обучения и воспитания личного состава Вооружённых Сил. Высылка, 1) вид уголовного наказания, заключающийся в удалении осуждённого из места его жительства с запрещением проживания в определённых местностях. Гелидиум (Gelidium), род красных водорослей; включает около 40 видов, обитающих в тёплых морях. Гирин (провинция в Китае) Гирин, Цзилинь, провинция в Северо-Восточном Китае. |
|