Стирлинга формула
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| СТА |
| СТВ |
| СТЕ |
| СТЁ |
| СТИ |
| СТЛ |
| СТО |
| СТР |
| СТУ |
| СТШ |
| СТЫ |
| СТЬ |
| СТЭ |
| СТЮ |
| СТЯ |
Стирлинга формула, формула, дающая приближённое выражение произведения п первых натуральных чисел (т. н. факториала) 1×2×...×n = n!, когда число п сомножителей велико. Стирлинга формула была найдена (без оценки погрешности) Дж. Стирлингом, опубликовавшим её в 1730. Стирлинга формула устанавливает приближённое равенство
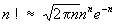 ,
,
где p = 3,14159..., е = 2,71828... (основание натуральных логарифмов), причём относительная ошибка при пользовании этой формулой для вычисления n! меньше e1/12n — 1 и, таким образом, стремится к нулю при неограниченном возрастании n. Например, при n = 10 Стирлинга формула даёт n!» 3598700, тогда как точное значение 10! = 3628800; относительная ошибка в данном случае составляет менее 1%. Стирлинга формула имеет многочисленные применения в приложениях математики, особенно в теории вероятностей и математической статистике.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.
|
Так же Вы можете узнать о... Файко Алексей Михайлович (р. 7(19).9.1893, Москва], русский советский драматург. Франко-советский договор 1944, см. Советско-французские соглашения. Хондроитинсерные кислоты, хондроитинсульфаты, полисахариды, составляющие основу хрящевой и костной ткани, роговицы и некоторых др. Червонопартизанск, город (с 1960) в Ворошиловградской области УССР, подчинён Свердловскому горсовету. Шишалдина вулкан, действующий вулкан на о. Унимак, наиболее высокая вершина Алеутских островов — 2860 м. Элементарная нить, одиночная нить, не делящаяся в продольном направлении без разрушения. Янушкевичюс Зигмас Ипполитович [р. 3(16).10. Акционерная коммандита, в буржуазных государствах вид компании (товарищества), соединяющий элементы акционерного общества и коммандитного товарищества. Антропоцентризм (от антропо... и лат. centrum — центр), воззрение, согласно которому человек есть центр и высшая цель мироздания. Аэрофотограмметрия, раздел фотограмметрии, занимающийся измерениями изображений объектов или участков местности на аэроснимках, полученных воздушным фотографированием. Белоярская атомная электростанция им. И. В. Курчатова, опытно-промышленная АЭС. |
|