Исчерпывания метод
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ИСА |
| ИСБ |
| ИСЕ |
| ИСИ |
| ИСК |
| ИСЛ |
| ИСМ |
| ИСО |
| ИСП |
| ИСР |
| ИСС |
| ИСТ |
| ИСФ |
| ИСХ |
| ИСЧ |
Исчерпывания метод, метод доказательства, применявшийся математиками древности при нахождении площадей и объёмов. Название «метод исчерпывания» введено в 17 в.
Рис. к ст. Исчерпывания метод.
Типичная схема доказательства при помощи Исчерпывания метод может быть изложена в современных обозначениях так: для определения величины А строится некоторая последовательность величин C1, C2, ..., Cn, ... так, что
Cn < A; (1)
предполагают также известным такое В, что
Cn<В (2)
и при любом целом К для достаточно больших n удовлетворяются неравенства
К (A — Cn) < D, К (В — Cn) < D, (3)
где D — постоянно. С современной точки зрения, для перехода от неравенств (3) к равенству
А = В (4)
достаточно заметить, что из условий (1), (2) и (3) следует 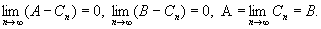
Математики древности, не располагавшие теорией пределов, обращались к доказательству от противного и доказывали невозможность каждого из неравенств А < В, В < А. Чтобы опровергнуть первое из них, при помощи аксиомы Евдокса — Архимеда (см. Архимеда аксиома) устанавливали, что для R = B — А существует такое К, что KR > D и в силу условия (1) получали К (В — Cn) >К (В — A) > D,
что противоречит второму из неравенств (3). Аналогично опровергалось другое предположение. После этого оставалось принять только равенство (4).
Введение Исчерпывания метод вместе с лежащей в его основе аксиомой приписывается Евдоксу Книдскому. Этим методом широко пользовался Евклид, а с особенным искусством и разнообразием — Архимед. Например, для определения площади сегмента А параболы Архимед строит площади C1, C2, ..., «исчерпывающие» при их постепенном нарастании площадь A сегмента, по схеме, ясной из чертежа. При этом 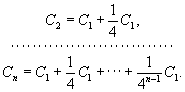
Вместо того чтобы прибегнуть к предельному переходу, 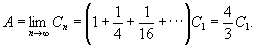
Архимед геометрически доказывает, что при любом n 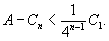
Вводя площадь 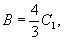
Архимед получает, что 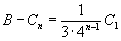
и, следуя изложенному выше порядку, заканчивает доказательство того, что 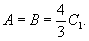
|
Так же Вы можете узнать о... Сутомо (Sutomo) (30.7.1888 — 30.5. 1938), деятель индонезийского национального движения. Таты, народность, населяющая прикаспийские районы в Азербайджанской ССР и южной части Дагестанской АССР. Тивериадское озеро, Генисаретское озеро, Галилейское озеро, Бахр-Табария, озеро в исторической области Палестина на территории Израиля (восточное побережье на границе Сирии и Израиля). Трансиордания, до 1946 название государства Иордания. Туффит, вулканогенно-осадочная горная порода, состоящая из вулканогенного материала, выброшенного при извержении вулкана (шлаков, пепла, пемзы, обломков пород), и смешанного с ним осадочного материала. Уралец, посёлок городского типа в Пригородном районе Свердловской обл. Феноло-альдегидные смолы, олигомерные продукты поликонденсации фенола, его гомологов (крезолов, ксиленолов) и многоатомных фенолов (например, резорцина) с альдегидами (формальдегидом и фурфуролом). Форма государства, в узком смысле форма правления, в широком смысле включает в себя также форму государственного устройства (унитарное государство, федерация, характер взаимоотношений между государством и его частями, между центральными и местными органами управления и др. Хамат, город и государство в Средней Сирии. Поселение существовало с эпохи неолита (4-е тыс. Хоментовский Александр Степанович [р. 11(24). Цианометр (от греч. kyanos — синий и ...метр), прибор, предназначенный для измерения цвета ясного дневного неба, разновидность колориметра. Чехословацко-польский договор 1967, см. Польско-чехословацкий договор 1967. Швингер Юлиус Швингер (Schwinger), Юлиус (Джулиус) (р. 12. Шум (физич.) Шум, беспорядочные колебания различной физической природы, отличающиеся сложностью временной и спектральной структуры. |
|