Максимального правдоподобия метод
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| МАА |
| МАБ |
| МАВ |
| МАГ |
| МАД |
| МАЕ |
| МАЁ |
| МАЖ |
| МАЗ |
| МАИ |
| МАЙ |
| МАК |
| МАЛ |
| МАМ |
| МАН |
| МАО |
| МАП |
| МАР |
| МАС |
| МАТ |
| МАУ |
| МАФ |
| МАХ |
| МАЦ |
| МАЧ |
| МАШ |
| МАЭ |
| МАЮ |
| МАЯ |
Максимального правдоподобия метод, метод нахождения статистических оценок неизвестных параметров распределения; согласно Максимального правдоподобия метод, в качестве оценок выбираются те значения параметров, при которых данные результаты наблюдений «наиболее вероятны». Предполагается, что результаты наблюдений X1, ..., Xn являются взаимно независимыми случайными величинами с одним и тем же распределением вероятностей, зависящим от одного неизвестного параметра qÎQ, где Q — множество допустимых значений q. Для придания точного смысла принципу «наибольшей вероятности» поступают следующим образом. Вводят функцию
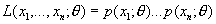 ,
,
где p(t; q) в случае непрерывного распределения интерпретируется как плотность вероятности случайной величины X, а в дискретном случае — как вероятность того, что случайная величина Х примет значение t. Функцию L(X1, . . ., Xn; q) от случайных величин X1, . . ., Xn называют функцией правдоподобия, а оценкой максимального правдоподобия параметра q называют такое значение 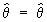 (X1, . . ., Xn) (само являющееся случайной величиной), при котором функция правдоподобия достигает наибольшего возможного значения. Так как точка максимума для log L та же, что и для L, то для нахождения оценок максимального правдоподобия следует решить так называемое уравнение правдоподобия
(X1, . . ., Xn) (само являющееся случайной величиной), при котором функция правдоподобия достигает наибольшего возможного значения. Так как точка максимума для log L та же, что и для L, то для нахождения оценок максимального правдоподобия следует решить так называемое уравнение правдоподобия
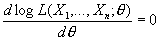 .
.
Максимального правдоподобия метод не всегда приводит к приемлемым результатам, однако в достаточно широком круге практически важных случаев этот метод является в известном смысле наилучшим. Так, например, можно утверждать, что если для параметра q существует несмещенная эффективная оценка q* по выборке объёма n, то уравнение правдоподобия имеет единств, решение 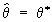 . Что касается асимптотического поведения оценок максимального правдоподобия при больших n, то известно, что при некоторых общих условиях Максимального правдоподобия метод приводит к состоятельной оценке, которая асимптотически нормальна и асимптотически эффективна. Данные выше определения непосредственно обобщаются и на случай нескольких неизвестных параметров и на случай выборок из многомерных распределений. Максимального правдоподобия метод в его современном виде был предложен английским статистиком Р. Фишером (1912), однако в частных формах метод использовался К. Гауссом, а ещё раньше, в 18 веке, к его идее были близки И. Ламберт и Д. Бернулли. Следует добавить, что название «Максимального правдоподобия метод» является калькой с английского «maximum likelihood method».
. Что касается асимптотического поведения оценок максимального правдоподобия при больших n, то известно, что при некоторых общих условиях Максимального правдоподобия метод приводит к состоятельной оценке, которая асимптотически нормальна и асимптотически эффективна. Данные выше определения непосредственно обобщаются и на случай нескольких неизвестных параметров и на случай выборок из многомерных распределений. Максимального правдоподобия метод в его современном виде был предложен английским статистиком Р. Фишером (1912), однако в частных формах метод использовался К. Гауссом, а ещё раньше, в 18 веке, к его идее были близки И. Ламберт и Д. Бернулли. Следует добавить, что название «Максимального правдоподобия метод» является калькой с английского «maximum likelihood method».
Лит.: Крамер Г., Математические методы статистики, перевод с английского, М., 1948; Рао С. Р., Линейные статистические методы и их применения, перевод с английского, М., 1968; Худсон Д., Статистика для физиков, перевод с английского, М., 1970.
А. В. Прохоров.
|
Так же Вы можете узнать о... Забелина Александра Ивановна (р. 11.3.1937, Москва), советская спортсменка (фехтование), заслуженный мастер спорта (1960). Иммерман Карл Лебрехт Иммерман (Immermann) Карл Лебрехт (24.4.1796, Магдебург, — 25. Кампонгсаом, Сиануквиль, город и порт в Камбодже, на берегу Сиамского залива. Кинопередвижка, портативная киноустановка для демонстрирования, в основном, узкопленочных (16-мм) кинофильмов в небольших зрительных залах, не оборудованных стационарными кинопроекционными установками. Контрерас Лабарка Карлос Контрерас Лабарка (Contreras Labarca) Карлос (р. Кузнецкий угольный бассейн, Кузбасс, один из самых крупных угольных бассейнов СССР и мира, вторая после Донецкого угольного бассейна угольная база СССР. Ли Юань-хун (19.10.1864, у. Хуанпи, пров. Хубэй, — 3. Малка, Балыксу, река в Кабардино-Балкарской АССР, левый приток реки Терек. Мехикали (Mexicali), город на северо-западе Мексики, на границе с США; административный центр штата Нижняя Калифорния. Мурманск (до апреля 1917 — Романов-на-Мурмане), город, центр ой области РСФСР. Нови (Novi), город в Италии (область Пьемонт), около которого 4(15) августа 1799 во время Итальянского похода Суворова 1799 русско-австрийского войска (65 тыс. Ортач Юсуф Зия Ортач (Ortac) Юсуф Зия (1895, Стамбул, — 11. |
|