Производная
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПРА |
| ПРЕ |
| ПРЁ |
| ПРЖ |
| ПРИ |
| ПРО |
| ПРУ |
| ПРШ |
| ПРЫ |
| ПРЮ |
| ПРЯ |
Производная, основное понятие дифференциального исчисления, характеризующее скорость изменения функции; Производная есть функция, определяемая для каждого х как предел отношения: 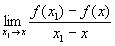 , если он существует. Функцию, имеющую Производная, называют дифференцируемой.
, если он существует. Функцию, имеющую Производная, называют дифференцируемой.
Всякая дифференцируемая функция непрерывна; обратное утверждение неверно: существуют даже непрерывные функции, не имеющие Производная ни в одной точке (см. Непрерывная функция). Для функций действительного переменного сама Производная может быть недифференцируемой и даже разрывной. В комплексной же области существование первой Производная влечёт существование Производная всех порядков. О Производная функций многих переменных (частная Производная), а также о правилах нахождения Производная и различных приложениях см. в ст. Дифференциальное исчисление.
В теории функций действительного переменного изучаются, в частности, функциональные свойства Производная и различные обобщения понятия «Производная». Так, например, всюду существующая Производная относится к функциям первого класса по Бэра классификации; Производная (даже если она разрывна) принимает все промежуточные значения между наименьшим и наибольшим. Из различных обобщений понятия «Производная» наиболее существенны следующие.
Производные числа. Верхним правым производным числом Dd называют верхний предел отношения 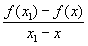 при
при  , где x1> х. Аналогично определяют нижнее правое ld, верхнее Ds и нижнее ls левые производные числа. Если Dd = ld (D = ls), то f (x) имеет в точке х одностороннюю правую (левую) Производная Обыкновенная Производная существует, если все четыре производных числа конечны и совпадают. Производные числа были введены итал. математиком У. Дини (1878). Как показал Н. Н. Лузин (1915), если все четыре производных числа конечны на некотором множестве, то функция имеет обычную Производная всюду на этом множестве, кроме точек множества меры нуль (см. Мера множества).
, где x1> х. Аналогично определяют нижнее правое ld, верхнее Ds и нижнее ls левые производные числа. Если Dd = ld (D = ls), то f (x) имеет в точке х одностороннюю правую (левую) Производная Обыкновенная Производная существует, если все четыре производных числа конечны и совпадают. Производные числа были введены итал. математиком У. Дини (1878). Как показал Н. Н. Лузин (1915), если все четыре производных числа конечны на некотором множестве, то функция имеет обычную Производная всюду на этом множестве, кроме точек множества меры нуль (см. Мера множества).
Асимптотическая (или аппроксимативная) производная была введена А. Я. Хинчиным(1916). Асимптотической Производная называется предел отношения 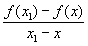 , когда x1®x пробегая точки множества, для которого х является плотности точкой.
, когда x1®x пробегая точки множества, для которого х является плотности точкой.
|
Так же Вы можете узнать о... Бесконечно малая в математике, переменная величина, стремящаяся к пределу, равному нулю. БЭСМ, быстродействующая электронная счётная машина, название серии цифровых вычислительных машин (ЦВМ), разработанных в Институте точной механики и вычислительной техники АН СССР. Войков Петр Лазаревич (партийный псевдоним Петрусь, Интеллигент) [1(13). Герман Яков (16.7.1678, Базель, — 14.7.1733, там же), первый академик-математик Петербургской АН (1725). Гуменник (Anser fabalis), птица отряда гусиных (Anseriformes). Долговременное огневое сооружение (ДОС), прочное (из камня, кирпича, бетона, железобетона, броневых конструкций и др. Зейст (Zeist), город в Нидерландах, в провинции Утрехт. Йодль (жанр нар. песен) Йодль, йодлер (нем. Jodel, Jodler, от jodein — петь с переливами на тирольский лад), жанр народных песен у альпийских горцев (в Австрии, Швейцарии, Южной Баварии), с рефреном в форме вокализа. Кесальтенанго (Quezaltenango), город в Гватемале, около Панамериканского шоссе, на высоте 2350 м; административный центр департамента . Копенгагенский мир 1660, был заключён между Данией и Швецией 27 мая в Копенгагене после неудачного для Швеции исхода датско-шведской войны 1658—60 и подписания ею Оливского мира 1660 с союзниками Дании. Кэлиман (Caliman), горный массив в Восточных Карпатах, на С. Лукреций Тит Лукреций, Тит Лукреций Кар (Titus Lucretius Carus) (1 век до н. Меликишвили Георгий Александрович (р. 30.12. Мукденское сражение 1905, крупная наступательная операция японских войск 6 (19) февраля — 25 февраля (10 марта) во время русско-японской войны 1904—05. Норидж, Норвич (Norwich), город в Великобритании, на р. |
|