Субгармонические функции
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| СУА |
| СУБ |
| СУВ |
| СУГ |
| СУД |
| СУЖ |
| СУЗ |
| СУИ |
| СУЙ |
| СУК |
| СУЛ |
| СУМ |
| СУН |
| СУО |
| СУП |
| СУР |
| СУС |
| СУТ |
| СУУ |
| СУФ |
| СУХ |
| СУЧ |
| СУШ |
| СУЩ |
| СУЫ |
| СУЭ |
| СУЮ |
Субгармонические функции, функции, удовлетворяющие в некоторой области неравенству
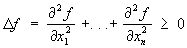 .
.
В случае, когда Df = 0, функция f является гармонической функцией. Понятие Субгармонические функции можно рассматривать как обобщение понятия гармонической функции. При n = 1 условие Df³ 0 принимает вид 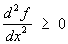 , то есть Субгармонические функции одного переменного есть выпуклая функция. Поэтому понятие Субгармонические функции можно рассматривать также как распространение понятия выпуклой функции на случай любого числа переменных. Так, например, подобно тому как всякая дуга графика выпуклой функции лежит ниже хорды, соединяющей её концы, всякая ограниченная некоторым контуром часть поверхности z = f (x, y), где f (x, у) — Субгармонические функции двух переменных, лежит ниже проходящей через тот же контур поверхности z = F (x, у), где F (x, у) — гармоническая функция (отсюда название «субгармоническая», то есть «подгармоническая»).
, то есть Субгармонические функции одного переменного есть выпуклая функция. Поэтому понятие Субгармонические функции можно рассматривать также как распространение понятия выпуклой функции на случай любого числа переменных. Так, например, подобно тому как всякая дуга графика выпуклой функции лежит ниже хорды, соединяющей её концы, всякая ограниченная некоторым контуром часть поверхности z = f (x, y), где f (x, у) — Субгармонические функции двух переменных, лежит ниже проходящей через тот же контур поверхности z = F (x, у), где F (x, у) — гармоническая функция (отсюда название «субгармоническая», то есть «подгармоническая»).
Приведённое выше определение предполагает, что функция f имеет частные производные второго порядка. От этого ограничения освобождаются, непосредственно выражая отмеченное только что свойство графика Субгармонические функции располагаться ниже графика гармонической функции.
Супергармонические функции (от лат. super — над) — функции, удовлетворяющие неравенству Df £ 0. Если f — супергармоническая функция, то f есть Субгармонические функции, и наоборот. Классические примеры Субгармонические функции и супергармонических функций: для n = 2 логарифмический потенциал
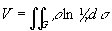
и для n = 3 объёмный потенциал
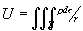
(здесь r— плотность масс или зарядов). Функции эти внутри областей G и Т удовлетворяют соответственно уравнениям Пуассона DV = — 2pr и DU = — 4prи, следовательно, являются супергармоническими при r³ 0 и Субгармонические функции при r < 0.
Субгармонические функции применяются, например, при решении задач математической физики (в частности, в теории потенциала), теории случайных процессов.
Лит.: Привалов И. И., Субгармонические функции, М.—Л., 1937.
|
Так же Вы можете узнать о... Ленкорань, город в Азербайджанской ССР. Расположен на Ленкоранской низменности, на левом берегу р. Майано (Maiano), семья итальянских архитекторов, скульпторов и резчиков по дереву. Мерная линия, мерная миля, участок акватории, предназначенный для проведения ходовых испытаний судов. Мотыга вращающаяся, машина для разрушения почвенной корки на посевах зерновых и технических культур, уничтожения сорняков, предпосевной обработки почвы, прореживания всходов сахарной свёклы. Никарагуанская социалистическая партия (Partido Socialista Nicaragüense; НСП), партия никарагуанских коммунистов, основана в 1939 на Национальной ассамблее, собравшейся с целью объединения марксистских групп и кружков, существовавших в стране с 20-х гг. Оптический отвес, геодезический оптический прибор; см. Пеммикан (англ. pemmican, заимствовано из языков индейцев алгонкинов), брикеты из сушёного и растёртого в порошок оленьего или бизоньего мяса, смешанного с жиром и соком кислых ягод. Полигалит (от поли... и греч. hals — соль), минерал, водный сульфат калия, кальция и магния, K2Ca2Mg [SO4]4. Прудовое рыбоводное хозяйство, хозяйство, разводящее быстро растущие виды рыб в специально построенных или приспособленных прудах. Решт, город в Иране, административный центр остана Гилян. Саскуэханна (Stisquebanna), река на В. США. Длина 990 км, площадь бассейна 71 тыс. Скин-эффект (от англ. skin — кожа, оболочка), поверхностный эффект, затухание электромагнитных волн по мере их проникновения в глубь проводящей среды, в результате которого, например, переменный ток по сечению проводника или переменный магнитный поток по сечению магнитопровода распределяются не равномерно, а преимущественно в поверхностном слое. |
|