Траектория (физич., математич.)
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ТРА |
| ТРД |
| ТРЕ |
| ТРЁ |
| ТРИ |
| ТРН |
| ТРО |
| ТРП |
| ТРУ |
| ТРШ |
| ТРЮ |
| ТРЯ |
Траектория (от позднелат. trajectorius — относящийся к перемещению), непрерывная линия, которую описывает точка при своём движении. Если Траектория (физич., математич.) — прямая линия, движение точки называется прямолинейным, в противном случае — криволинейным. Вид Траектория (физич., математич.) свободной материальной точки зависит от действующих на точку сил, начальных условий движения и от того, по отношению к какой системе отсчёта движение рассматривается; для несвободной точки вид Траектория (физич., математич.) зависит ещё от наложенных связей (см. Связи механические).
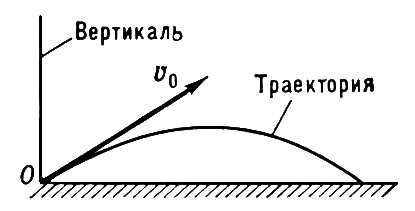
Например, по отношению к Земле (если пренебречь её суточным вращением) Траектория (физич., математич.) свободной материальной точки, отпущенной без начальной скорости и движущейся под действием силы тяжести, будет прямая линия (вертикаль), а если точке сообщить начальную скорость u0, не направленную вдоль вертикали, то при отсутствии сопротивления воздуха её Траектория (физич., математич.) будет парабола (рис. 1).
Рис. 1. Параболическая траектория.
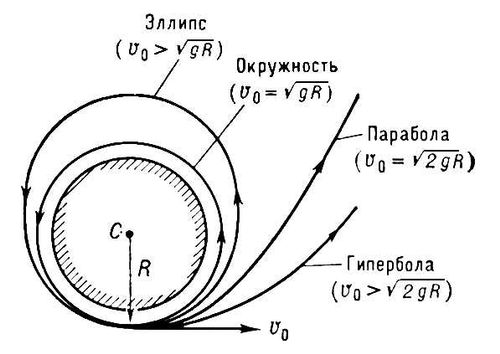
Траектория (физич., математич.) точки, движущейся в центральном поле тяготения, в зависимости от величины начальной скорости может быть эллипс, парабола или гипербола (в частных случаях — прямая линия или окружность). Так, в поле тяготения Земли, если считать его центральным и пренебречь сопротивлением среды, Траектория (физич., математич.) точки, получившей вблизи поверхности Земли начальную скорость u0, направленную горизонтально (рис. 2), будет: окружность, когда 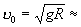 7,9 км/сек (первая космическая скорость); эллипс, когда
7,9 км/сек (первая космическая скорость); эллипс, когда 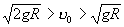 ; парабола, когда
; парабола, когда 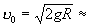 11,2 км/сек (вторая космическая скорость) и гипербола, когда
11,2 км/сек (вторая космическая скорость) и гипербола, когда 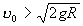 . Здесь R — радиус Земли, g— ускорение силы тяготения вблизи земной поверхности, а движение рассматривается по отношению к осям, перемещающимся вместе с центром Земли поступательно относительно звёзд; для тела (например, спутника) всё сказанное относится к Траектория (физич., математич.) его центра тяжести. Если же направление u0 не будет ни горизонтальным, ни вертикальным, то при
. Здесь R — радиус Земли, g— ускорение силы тяготения вблизи земной поверхности, а движение рассматривается по отношению к осям, перемещающимся вместе с центром Земли поступательно относительно звёзд; для тела (например, спутника) всё сказанное относится к Траектория (физич., математич.) его центра тяжести. Если же направление u0 не будет ни горизонтальным, ни вертикальным, то при 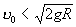 Траектория (физич., математич.) точки будет представлять собой дугу эллипса, пересекающую поверхность Земли; таковы Траектория (физич., математич.) центра тяжести баллистических ракет.
Траектория (физич., математич.) точки будет представлять собой дугу эллипса, пересекающую поверхность Земли; таковы Траектория (физич., математич.) центра тяжести баллистических ракет.
Рис. 2. Виды траекторий в поле тяготения Земли.
Пример несвободной точки — небольшой груз, подвешенный на нити (см. Маятник). Если нить отклонить от вертикали и отпустить без начальной скорости, то Траектория (физич., математич.) груза будет дугой окружности, а если при этом грузу сообщить начальную скорость, не лежащую в плоскости отклонения нити, то Траектория (физич., математич.) груза могут быть кривые довольно сложного вида, лежащие на поверхности сферы (сферический маятник), но в частном случае это может быть окружность, лежащая в горизонтальной плоскости (конический маятник).
Траектория (физич., математич.) точек твёрдого тела зависят от закона движения тела. При поступательном движении тела Траектория (физич., математич.) всех его точек одинаковы, а во всех других случаях движения эти Траектория (физич., математич.) будут вообще разными для разных точек тела. Например, у колеса автомобиля на прямолинейном участке пути Траектория (физич., математич.) точки обода колеса по отношению к шоссе будет циклоида, а Траектория (физич., математич.) центра колеса — прямая линия. По отношению же к кузову автомобиля Траектория (физич., математич.) точки обода будет окружность, а центр колеса — неподвижен.
Определение Траектория (физич., математич.) имеет важное значение как при теоретических исследованиях, так и при решении многих практических задач.
С. М. Тарг.
|
Так же Вы можете узнать о... «Наука и жизнь», ежемесячный научно-популярный иллюстрированный журнал широкого профиля, орган Всесоюзного общества «Знание» (с 1948). Прокуратор (лат. procurator, буквально— попечитель, управитель), в Древнем Риме 1) домоуправитель. Статский советник в России, гражданский чин 5-го класса по Табели о рангах, соответствовал должности вице-директора департамента, вице-губернатора, председателя казённой палаты и др. Химотрипсин, фермент класса гидролаз, расщепляющий белки и пептиды; содержится в секрете поджелудочной железы животных и человека. Анабарский залив, в западной части моря Лаптевых, между берегом материка и полуостровом Нордвик. Водонапорные системы, бассейны подземных вод, выделяемые с учётом всех закономерностей формирования и распространения подземных вод. Ергак-Таргак-тайга, Тазарама, горный хребет в системе Запалного Саяна, на стыке с Восточным Саяном, между верховьями рр. Кооперирование крестьянских хозяйств, процесс вовлечения мелких раздробленных крестьянских хозяйств в различные формы кооперативов. Мндоянц Ашот Ашотович [28.12.1909(10.1.1910), Батуми, — 29. Повальное воспаление лёгких крупного рогатого скота, плевропневмония, перипневмония (ПВЛ), инфекционная болезнь, протекающая в виде крупозной пневмонии с воспалением междольковой соединительной ткани и лимфатических сосудов, возникновением анемических некрозов и секвестров, а также серозно-фибринозного плеврита. Сколекодонты (Scolecodonten), ископаемые остатки челюстей хищных многощетинковых червей. Фестука, род растений семейства злаков; то же, что овсяница. Авиационная астрономия, раздел практической астрономии, в котором рассматриваются методы астрономической навигации в полёте. Васильченко Степан Васильевич Васильченко (псевдоним; настоящая фамилия Панасенко) Степан Васильевич [27. |
|