Управляемый случайный процесс
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| УПА |
| УПД |
| УПЕ |
| УПИ |
| УПК |
| УПЛ |
| УПО |
| УПР |
| УПС |
| УПТ |
| УПУ |
| УПЫ |
Управляемый случайный процесс, случайный процесс, вероятностные характеристики которого можно изменять с помощью управляющих воздействий. Основная цель теории Управляемый случайный процесс – отыскание оптимальных (или близких к ним) управлений, доставляющих экстремум заданному критерию качества. В простейшем случае управляемых марковских цепей одна из математических постановок задачи нахождения оптимального управления формулируется следующим образом. Пусть Xd = (xn,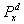 ), n = 0, 1,..., – семейство однородных марковских цепей с конечным числом состояний Е = {0, 1, ..., N} и матрицами переходных вероятностей Pxy (d) =
), n = 0, 1,..., – семейство однородных марковских цепей с конечным числом состояний Е = {0, 1, ..., N} и матрицами переходных вероятностей Pxy (d) = 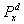 {x1 = у}, зависящих от параметра d, принадлежащего некоторому множеству управляющих воздействий D. Набор функций a = {а0 (x0), a1 (x0, x1),...} со значениями в D называют стратегией, а каждую из функций an = ап (х0,..., хп) – управлением в момент времени n. Каждой стратегии a отвечает управляемая марковская цепь Xa = (хп,
{x1 = у}, зависящих от параметра d, принадлежащего некоторому множеству управляющих воздействий D. Набор функций a = {а0 (x0), a1 (x0, x1),...} со значениями в D называют стратегией, а каждую из функций an = ап (х0,..., хп) – управлением в момент времени n. Каждой стратегии a отвечает управляемая марковская цепь Xa = (хп,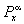 ), n = 0, 1,..., где
), n = 0, 1,..., где
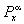 (x0, x1..., хп) = d(х0, х) Рх0х1 (a0 (x0))... Pxn-1xn (an-1(x0, x1,..., xn-1))
(x0, x1..., хп) = d(х0, х) Рх0х1 (a0 (x0))... Pxn-1xn (an-1(x0, x1,..., xn-1))
Пусть: 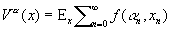
где функция f (d, х)³0 и f (d,0) = 0 (если точка {0} является поглощающим состоянием и f (d, x) = I, d ÎD, x = 1,..., N, то Va (x) есть матем. ожидание времени попадания из точки х в точку 0). Функцию

называется ценой, а стратегию а* – оптимальной, если 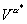 = V (x) для всех х ÎЕ.
= V (x) для всех х ÎЕ.
При довольно общих предположениях о множестве D устанавливается, что цена V (x) удовлетворяет следующему уравнению оптимальности (уравнению Беллмана):
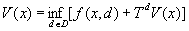 ,
,
где
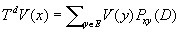 .
.
В классе всех стратегий наибольший интерес представляют т. н. однородные марковские стратегии, характеризуемые одной функцией а (х) такой, что an (x0,..., xn) = a (xn) при всех n = 0, 1,...
Следовательно, критерий оптимальности (или достаточное условие оптимальности) может быть использован для проверки того, что данная однородная марковская стратегия является оптимальной: пусть существуют функции a* = а*(х) и V* = V*(x) такие, что для любого d ÎD
0 = f (x, a*(x)) + La*V*£f (x, d) + LdV*(x)
(Ld = Td – I, I – единичный оператор), тогда V* является ценой (V* = V) и стратегия a* = a*(х) является оптимальной.
Лит.: Ховард Р.-А., Динамическое программирование и марковские процессы, пер. с англ., М. 1964.
А. Н. Ширяев.
|
Так же Вы можете узнать о... Внушение (психологич.) Внушение, в широком смысле слова — воздействие на личность, приводящее либо к появлению у человека, помимо (а иногда и против) его воли и сознания, определённого состояния (например, бодрости, уверенности), чувства (например, страха), отношения (к объекту, к самому себе, к своему состоянию), либо к совершению человеком поступка, непосредственно не следующего из принимаемых им норм и принципов деятельности. Встречные перевозки, перевозки грузов в обратном направлении по отношению к нормальному потоку таких же (однородных, взаимозаменяемых) грузов. Гаркуша Илья (гг. рождения и смерти неизвестны), один из руководителей борьбы белорусского народа против польских феодалов в 1648, развернувшейся одновременно с освободительной войной на Украине. Гёзы (голл. geuzen, от франц. gueux — нищие), в период Нидерландской буржуазной революции 16 века: 1) прозвище членов Союза дворян, образованного оппозиционной знатью в 1565 с целью защиты «законными средствами» вольностей страны от посягательств испанского абсолютизма; 2) прозвище народных партизан, которые на суше (лесные Г. Голубянки (Lycaenidae), семейство дневных бабочек. Гринченко Борис Дмитриевич [27.11(9.12). 1863, хутор Вильховий Яр на Харьковщине, — 23. Двина Северная, река на С. Европейской части СССР; см. Джесселтон (Jesselton), город в Малайзии; см. «Дом свободного ребёнка», школа экспериментального типа для детей от 5 до 10 лет; была организована в 1906 членами Московского кружка совместного воспитания и образования (во главе с К. Елисеев Николай Александрович [7(19).12.1897, Самара, ныне Куйбышев, — 24. |
|