Ферма принцип
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ФЕА |
| ФЕБ |
| ФЕВ |
| ФЕД |
| ФЕЕ |
| ФЕЙ |
| ФЕК |
| ФЕЛ |
| ФЕМ |
| ФЕН |
| ФЕО |
| ФЕР |
| ФЕС |
| ФЕТ |
| ФЕФ |
| ФЕХ |
| ФЕЦ |
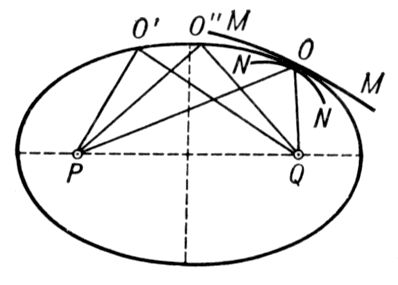
Ферма принцип, основной принцип геометрической оптики. Простейшая форма Ферма принцип – утверждение, что луч света всегда распространяется в пространстве между двумя точками по тому пути, по которому время его прохождения меньше, чем по любому из всех др. путей, соединяющих эти точки. Время прохождения светом расстояния l, заполненного средой с преломления показателем n, пропорционально оптической длине пути S; S = 1•n для однородной среды, а при переменном n 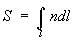 . Поэтому можно сказать, что Ферма принцип есть принцип наименьшей оптической длины пути. В первоначальной формулировке самого П. Ферма (около 1660) Ферма принцип имел смысл наиболее общего закона распространения света, из которого следовали все (к тому времени уже известные) законы геометрической оптики: для однородной среды он приводит к закону прямолинейности светового луча (в соответствии с геометрическим положением о том, что прямая есть кратчайшее расстояние между двумя точками), а для случая падения луча на границу различных сред из Ферма принцип можно получить законы отражения света и преломления света. В более строгой формулировке Ферма принцип представляет собой вариационный принцип, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, по которой время его прохождения экстремально или одинаково по сравнению с временами прохождения по всем др. линиям, соединяющим эти точки. Это означает, что оптическая длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям, соединяющим указанные точки. Примерами минимального пути служат упомянутые распространение света в однородной среде и прохождение светом границы двух сред с разными показателями преломления n. Все три случая (минимальности, максимальности и стационарности пути) можно проиллюстрировать, анализируя отражение луча света от вогнутого зеркала (рис.).
. Поэтому можно сказать, что Ферма принцип есть принцип наименьшей оптической длины пути. В первоначальной формулировке самого П. Ферма (около 1660) Ферма принцип имел смысл наиболее общего закона распространения света, из которого следовали все (к тому времени уже известные) законы геометрической оптики: для однородной среды он приводит к закону прямолинейности светового луча (в соответствии с геометрическим положением о том, что прямая есть кратчайшее расстояние между двумя точками), а для случая падения луча на границу различных сред из Ферма принцип можно получить законы отражения света и преломления света. В более строгой формулировке Ферма принцип представляет собой вариационный принцип, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, по которой время его прохождения экстремально или одинаково по сравнению с временами прохождения по всем др. линиям, соединяющим эти точки. Это означает, что оптическая длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям, соединяющим указанные точки. Примерами минимального пути служат упомянутые распространение света в однородной среде и прохождение светом границы двух сред с разными показателями преломления n. Все три случая (минимальности, максимальности и стационарности пути) можно проиллюстрировать, анализируя отражение луча света от вогнутого зеркала (рис.).
К принципу Ферма: действительный путь света соответствует экстремальному времени распространения.
К принципу Ферма: действительный путь света соответствует экстремальному времени распространения.
Если зеркало имеет форму эллипсоида вращения, а свет распространяется от одного его фокуса Р к другому Q (причём путь без отражения невозможен), то оптическая длина пути луча PO' + O'Q по свойствам эллипсоида равна всем остальным возможным, например PO'' + О''Q; если на пути между теми же точками свет отражается от зеркала меньшей, чем у эллипсоида, кривизны (MM), реализуется минимальный путь, если же большей (зеркало NN) – максимальный. Условие экстремальности оптической длины пути сводится к требованию, чтобы была равна нулю вариация от интеграла 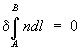 (см. Вариационное исчисление), где А и В – точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ферма принцип
(см. Вариационное исчисление), где А и В – точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ферма принцип
В волновой теории света Ферма принцип представляет собой предельный случай Гюйгенса – Френеля принципа и применим, когда можно пренебречь дифракцией света (когда длина световой волны достаточно мала по сравнению с характерными для задачи размерами): рассматривая лучи как нормали к волновым поверхностям, легко показать, что при всяком распространении света оптической длины их путей будут иметь экстремальные значения. Во всех случаях, когда необходимо учитывать дифракцию, Ферма принцип перестаёт быть применимым.
Лит.: Fermat P. de, CEuvres, t. 1–4, P., 1891–1912; Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Крауфорд Ф., Волны, М., 1974 (Берклеевский курс физики, т. 3); Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973.
А. П. Гагарин.
|
Так же Вы можете узнать о... Бровка Петрусь (Петр Устинович) [р. 12(25).6. Грудница (мед.) Грудница (медицинская), воспаление грудной (правильнее — молочной) железы; то же, что мастит. Казановка, посёлок городского типа в Кимовском районе Тульской области РСФСР. Левченко Гордей Иванович [р. 20.1(1.2).1897, Дубровка, ныне Барановского района Житомирской области], советский военно-морской деятель, адмирал (1944). Неисправность, состояние технического устройства, при котором хотя бы один из его основных или дополнительных параметров не соответствует требованиям, обусловленным технической документацией. Преобразовательная подстанция, подстанция электрическая для преобразования электрического тока, преимущественно по частоте и числу фаз. Соединённых Штатов Америки и Канады институт, институт Соединенных Штатов Америки и Канады АН СССР, научно-исследовательское учреждение, изучающее экономику, социальные отношения, внутреннюю и внешнюю политику США и Канады. Фесенков Василий Григорьевич [1(13).1.1889, Новочеркасск, – 12. Юго-Восточный мыс (South East Point), крайняя южная точка материка Австралия под 39° 11' южной широты Бокхорис (греч. Bokchoris, др.-егип. — Бекенренеф), в Древнем Египте фараон XXIV династии, правивший в 732—726 до н. Горные институты, вузы, готовящие инженеров для работы в горнодобывающих отраслях промышленности — угольной, торфяной, добычи руд чёрных, цветных и редких металлов, химического сырья и строительных материалов, нефтяной и газовой. Ионогальванизация, физиотерапевтический метод лечения; то же, что электрофорез лекарственный. Кыштымские волнения 1822 - 1823 Кыштымские волнения 1822—1823, волнения рабочих Кыштымских и Каслинского металлургических заводов купца Расторгуева в Пермской губернии. Нагаока, город в Японии, в центральной части острова Хонсю, в префектуре Ниигата, на р. Поляризованные ядра, см. Ориентированные ядра. Скополия (Scopolia), род растений семейства паслёновых. |
|