Функции множества
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ФУА |
| ФУВ |
| ФУГ |
| ФУД |
| ФУЖ |
| ФУЗ |
| ФУК |
| ФУЛ |
| ФУМ |
| ФУН |
| ФУР |
| ФУС |
| ФУТ |
| ФУЦ |
| ФУЧ |
| ФУШ |
| ФУЭ |
Функции множества, функции, сопоставляющие каждому множеству из некоторого класса множеств определённое число. Например, длина отрезка является Функции множества, определённой на классе всех отрезков на прямой (функцией отрезка).
Интеграл 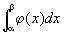 при заданной интегрируемой функции j(x) также является функцией отрезка — интервала интегрирования [a, b]. Рассматривают также функции от областей на плоскости или в пространстве. Например, при заданном распределении плотностей масса, заключённая в данной области W, является функцией этой области. Понятие функции области — более гибкий аппарат для описания физических явлений, чем понятие функции точки, т.к. позволяет учитывать случаи, когда плотность физических величин в отдельных точках бесконечна (точечные источники и т.д.). Кроме того, это понятие более отвечает условиям физического эксперимента (при котором наблюдается не функция точки, а среднее от этой функции по некоторой малой области).
при заданной интегрируемой функции j(x) также является функцией отрезка — интервала интегрирования [a, b]. Рассматривают также функции от областей на плоскости или в пространстве. Например, при заданном распределении плотностей масса, заключённая в данной области W, является функцией этой области. Понятие функции области — более гибкий аппарат для описания физических явлений, чем понятие функции точки, т.к. позволяет учитывать случаи, когда плотность физических величин в отдельных точках бесконечна (точечные источники и т.д.). Кроме того, это понятие более отвечает условиям физического эксперимента (при котором наблюдается не функция точки, а среднее от этой функции по некоторой малой области).
Понятие Функции множества получило развитие в связи с построением теории интеграла Лебега, в которой приходится рассматривать не только функции от областей, но и функции от произвольных измеримых множеств. Одним из первых примеров такой Функции множества является мера Лебега m(Е) измеримого множества Е (см. Мера множества). Эта Функции множества вполне аддитивна, т. е. мера суммы любой конечной или счётной совокупности непересекающихся измеримых множеств есть сумма мер этих множеств. Наряду с лебеговской мерой множеств рассматривают др. меры, являющиеся неотрицательными вполне аддитивными Функции множества, определёнными на соответствующем классе множеств. Такие Функции множества встречаются в общей теории интеграла. Функции множества f (E) называют абсолютно непрерывной относительно некоторой меры m, если f (E) = 0 при m(Е) = 0. Так, интеграл Лебега 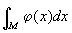 заданной суммируемой функции j(x) по множеству М является вполне аддитивной абсолютно непрерывной (относительно меры Лебега) функцией от М. Обратно, всякая вполне аддитивная абсолютно непрерывная Функции множества может быть представлена в качестве интеграла Лебега от некоторой суммируемой функции j(x). Важным примером Функции множества являются распределения вероятностей.
заданной суммируемой функции j(x) по множеству М является вполне аддитивной абсолютно непрерывной (относительно меры Лебега) функцией от М. Обратно, всякая вполне аддитивная абсолютно непрерывная Функции множества может быть представлена в качестве интеграла Лебега от некоторой суммируемой функции j(x). Важным примером Функции множества являются распределения вероятностей.
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976; Халмош П., Теория меры, пер. с англ., М., 1953
|
Так же Вы можете узнать о... Адамсон Амандус Генрих [31.10(12.11).1855, хутор Ууга-Рятсепа, близ Палдиски, — 26. Гиннекен Якобус Иоаннес Антониус ван Гиннекен (Ginneken) Якобус Иоаннес Антониус ван (21. Колхозное право, отрасль социалистического права, представляющая собой совокупность установленных либо санкционированных Советским государством правовых норм, закрепляющих основные принципы, формы и порядок организации и деятельности колхозов, регулирующих их отношения с членами колхоза, семьями колхозников и колхозными дворами, регламентирующих организацию и деятельность выборных колхозных органов, а также межколхозных предприятий, организаций и их объединений (см. Нуль (от лат. nullus — никакой), число, обладающее тем свойством, что любое число при сложении с ним не меняется. Сковородино (до 1938 — Рухлово), город, центр Сковородинского района Амурской области РСФСР. Шарнирный механизм ,механизм, звенья которого образуют только вращательные кинематические пары (шарниры). Верховинцы, название украинцев, живущих на обоих склонах Карпат в пределах УССР и частично в Чехословакии. Кави (санскр. — поэт), древнеяванский литературный язык, оформившийся во 2-й половине 1-го тыс. Мокрота, патологические выделения из дыхательных путей, отходящие при кашле; продукт избыточной активности слизистых желёз. Росичка (Digitaria), род одноили многолетних трав семейства злаков. |
|