Линейное программирование
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ЛИА |
| ЛИБ |
| ЛИВ |
| ЛИГ |
| ЛИД |
| ЛИЕ |
| ЛИЗ |
| ЛИЙ |
| ЛИК |
| ЛИЛ |
| ЛИМ |
| ЛИН |
| ЛИО |
| ЛИП |
| ЛИР |
| ЛИС |
| ЛИТ |
| ЛИУ |
| ЛИФ |
| ЛИХ |
| ЛИЦ |
| ЛИЧ |
| ЛИШ |
при условиях
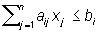 , i = 1, 2, ..., m, (2)
, i = 1, 2, ..., m, (2)
xj³ 0, j = 1, 2, n, (3)
где cj, aij и bi — заданные величины.
Задачи Л. п. являются математическими моделями многочисленных задач технико-экономического содержания. Рассмотрим в качестве примера следующую задачу планирования работы предприятия. Для производства однородных изделий необходимо затратить различные производственные факторы — сырьё, рабочую силу, станочный парк, топливо, транспорт и т. д. Обычно имеется несколько отработанных технологических способов производства, причём в этих способах затраты производственных факторов в единицу времени для выпуска изделий различны. Количество израсходованных производственных факторов и количество изготовленных изделий зависит от того, сколько времени предприятие будет работать по тому или иному технологическому способу. Ставится задача рационального распределения времени работы предприятия по различным технологическим способам, т. е. такого, при котором будет произведено максимальное количество изделий при заданных ограниченных затратах каждого производственного фактора. Формализуем задачу. Пусть имеется n технологических способов производства изделий и m производственных факторов. Введём обозначения: cj— количество изделий, выпускаемых в единицу времени при работе по j-му технологическому способу; aij— расход i-го производственного фактора в единицу времени при работе по j-му технологическому способу; bi — имеющиеся ресурсы i-го производственного фактора и xj— планируемое время работы по j-му технологическому способу. Величина
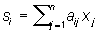
означает общий расход i-го производственного фактора при плане х(i) = (x(i)1, x(i)2, ..., x(i)n). И поскольку ресурсы ограничены величинами bi, то возникают естественные условия (2) и (3). Ставится задача отыскания такого распределения времени (оптимального плана) х* = (x*1, х*2, ..., х* n) работы по каждому технологическому способу, при котором общий объём продукции 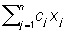 был бы максимальным, то есть задача (1) — (3). Другим характерным примером прикладных задач Л. п. является транспортная задача.
был бы максимальным, то есть задача (1) — (3). Другим характерным примером прикладных задач Л. п. является транспортная задача.
Термин «Л. п.» нельзя признать удачным, однако смысл его в том, что в Л. п. решаются задачи составления оптимальной программы (плана) действий. В связи с этим Л. п. можно рассматривать как один из математических методов в исследованиях операций (см. Операций исследование).
Функцию (1) в Л. п. принято называть целевой функцией, или критерием эффективности, вектор х = (x1, x2, ..., xn) — планом, вектор x*=(x*1, x*2, ..., x*n) — оптимальным планом, а множество, определяемое условиями (2) — (3), — допустимым, или множеством планов. Одним из основных методов решения задач Л. п. является симплексный метод. Геометрически его идея состоит в следующем. Допустимое множество (2) — (3) представляет собой выпуклое многогранное множество (если оно ограничено, то — многомерный выпуклый многогранник). Если задача Л. п. имеет решение, то существует вершина х* многогранного множества, являющаяся оптимальным планом. Симплексный метод состоит в таком направленном переборе вершин, при котором значение целевой функции возрастает от вершины к вершине. Каждой вершине соответствует система уравнений, выбираемая спец. образом из системы неравенств (2) — (3), поэтому вычислительная процедура симплексного метода состоит в последовательном решении систем линейных алгебраических уравнений. Простота алгоритма делает этот метод удобным для его реализации на ЭВМ.
Лит.: Юдин Д. Б., Гольштейн Е. Г., Линейное программирование, М., 1969.
В. Г. Карманов.
|
Так же Вы можете узнать о... Канцонетта (итал. canzonetta — песенка, уменьшительное от canzone), в 16—17 вв. «Ковент-Гарден» [Covent Garden; полное название «Королевский оперный театр К. Кратон (от греч. krátos — сила, крепость), консолидированные участки земной коры, неспособные к преобразованию альпинотипной складчатостью (см. Ленуар Этьенн Ленуар (Lenoir) Этьенн [12.1.1822, Мюсси-ла-Виль, Люксембург, — 4 (по др. Маме, индейский народ, живущий в Гватемале и Мексике. Мироновский, посёлок городского типа в Донецкой обл. Нация (от лат. natio — племя, народ), историческая общность людей, складывающаяся в ходе формирования общности их территории, экономических связей, литературного языка, некоторых особенностей культуры и характера, которые составляют её признаки. Олигодоны (Oligodon), род неядовитых змей семейства ужей. Первичные половые признаки, совокупность особенностей, определяющих основные различия между самцом и самкой у животных, а также между мужчиной и женщиной. Попович Титус Попович (Popovici) Титус (р. 16.5.1930, Орадя), румынский писатель и сценарист. Размножитель-реактор ,ядерный реактор, в котором в результате взаимодействия 238U (или 232Th) с нейтронами, образующимися при делении 239Pu (233U) — первичного ядерного топлива, происходит накопление 239Pu (233U)— вторичного ядерного топлива. Саз, азербайджанский струнный щипковый музыкальный инструмент. Синхротронное излучение, магнитотормозное излучение, излучение электромагнитных волн заряженными частицами, движущимися с релятивистскими скоростями в магнитном поле. Стационарный искусственный спутник Земли, спутник, движущийся в экваториальной плоскости Земли по круговой орбите с угловой скоростью, равной угловой скорости вращения Земли. Тепловой удар (мед.) Тепловой удар, тепловая лихорадка, острое заболевание человека и животных, обусловленное расстройствами терморегуляции при длительном воздействии на организм высокой температуры внешней среды. Угольный микрофон ,микрофон, в котором для преобразования звуковых колебаний в электрические используется угольный порошок. |
|