Периодические решения
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПЕА |
| ПЕБ |
| ПЕВ |
| ПЕГ |
| ПЕД |
| ПЕЕ |
| ПЕЖ |
| ПЕЗ |
| ПЕЙ |
| ПЕК |
| ПЕЛ |
| ПЕМ |
| ПЕН |
| ПЕО |
| ПЕП |
| ПЕР |
| ПЕС |
| ПЕТ |
| ПЕХ |
| ПЕЦ |
| ПЕЧ |
| ПЕШ |
| ПЕЩ |
Периодические решения уравнений, решения, описывающие правильно повторяющиеся процессы. Для теории колебаний, небесной механики и др. наук особый интерес представляют Периодические решения системы дифференциальных уравнений
Рис. к ст. Периодические решения.
 , i = 1,..., n (1)
, i = 1,..., n (1)
Это такие решения yi = ji (t), которые состоят из периодических одного и того же периода функций независимого переменного t, то есть для всех значений t
ji (t + t) = ji (t)
где t > 0—период решения. Если система (1) стационарна, то есть функции fi = Fi (yi,.... yn), где i = 1,..., n, явным образом не зависят от t, то в фазовом пространстве (yi,..., yi) Периодические решения отвечают замкнутые траектории. В частном случае эти траектории могут вырождаться в точки покоя 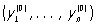 , где
, где 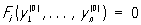 , которым соответствуют тривиальные (постоянные) Периодические решения Что касается нетривиальных Периодические решения, то задача о нахождении их решена лишь для дифференциальных уравнений специальных типов.
, которым соответствуют тривиальные (постоянные) Периодические решения Что касается нетривиальных Периодические решения, то задача о нахождении их решена лишь для дифференциальных уравнений специальных типов.
В теории нелинейных колебаний особое значение имеет система двух уравнений
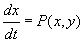 ,
, 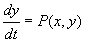 (2)
(2)
фазовым пространством которой является плоскость (х, у). Точки покоя системы (2) находятся из системы уравнений: Р (х, у) = 0, Q (x, у) = 0. Система (2) заведомо не допускает нетривиальных Периодические решения, если 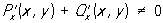 (критерий Бендиксона). Обычным приёмом обнаружения нетривиальных Периодические решения системы (2) (если они существуют) является построение такой ограниченной кольцеобразной области K (см. рис.), что все траектории входят в неё при t ® +¥ или при t ® -¥; если область К не содержит точек покоя системы (2), то в К обязательно найдётся замкнутая траектория, которой соответствует нетривиальное Периодические решения (принцип Пуанкаре — Бендиксона). Другой подход к обнаружению Периодические решения даёт изучение поведения решений в окрестностях особых точек; именно, в окрестности центра интегральные кривые системы (2) замкнуты и им соответствуют нетривиальные Периодические решения
(критерий Бендиксона). Обычным приёмом обнаружения нетривиальных Периодические решения системы (2) (если они существуют) является построение такой ограниченной кольцеобразной области K (см. рис.), что все траектории входят в неё при t ® +¥ или при t ® -¥; если область К не содержит точек покоя системы (2), то в К обязательно найдётся замкнутая траектория, которой соответствует нетривиальное Периодические решения (принцип Пуанкаре — Бендиксона). Другой подход к обнаружению Периодические решения даёт изучение поведения решений в окрестностях особых точек; именно, в окрестности центра интегральные кривые системы (2) замкнуты и им соответствуют нетривиальные Периодические решения
Лит.: Немыцкий В. В. и Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М.— Л., 1949; Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 2 изд., М., 1959; Стокер Дж., Нелинейные колебания в механических и электрических системах, пер. с англ., 2 изд., М., 1953.
|
Так же Вы можете узнать о... ФЗУ школа, см. Школа фабрично-заводского ученичества. Энгельман Теодор Вильгельм Энгельман (Engelmann) Теодор Вильгельм (14.11. Беллинсгаузен (науч. станция) Беллинсгаузен, научная станция на о. Кинг-Джордж (Ватерлоо) в группе Южных Шетлендских островов, первая советская станция у берегов Западной Антарктиды. Гварини Гварино Гварини, Гуарини (Guarini) Гварино (17.1.1624, Модена, — 6. «Журнал министерства путей сообщения», орган министерства путей сообщения России. Комаровский Александр Николаевич [р. 7(20).5. Маррамбиджи (Murrumbidgee), река на юго-востоке Австралии, правый приток реки Муррей. Опришки, украинские повстанцы, боровшиеся против феодально-крепостнического и национального гнёта в западных районах Украины (Галичина, Буковина, Закарпатье) в 16 — 1-й половины 19 вв. Рамзай Уильям Рамзай (правильнее Рэмзи; Ramsay) Уильям (2. Статуя (лат. statua), один из основных видов скульптуры, скульптурное изображение человеческой фигуры или животного (реже какого-либо фантастического существа), обычно помещенное на постамент. Форма (биол.) Форма (forma), одна из инфраподвидовых категорий в систематике растений и животных. Юзефович Иосиф Сигизмундович (6.7.1890 — 12. Биплан (от би... и лат. planum — плоскость), самолёт с двумя крыльями, расположенными одно над другим. Гидро... (от греч. hydor — вода), начальная часть сложных слов, указывающая на отношение их к воде, водоёмам и т. Зеркальный карп, самая распространённая форма разводимого в прудах карпа (культурная форма сазана). Корабль (архитект.) Корабль в архитектуре, то же, что неф. Мел (единица высоты звука) Мел, внесистемная единица высоты звука, применяется главным образом в музыкальной акустике. Охридское озеро (Ohridsko jezero, ligeni i Ohrit), озеро в Югославии и Албании. Рефлексология, естественнонаучное направление в психологии, получившее развитие в период 1900—30, главным образом в России, и связанное с деятельностью В. |
|
