Целая функция
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ЦЕА |
| ЦЕБ |
| ЦЕВ |
| ЦЕГ |
| ЦЕД |
| ЦЕЗ |
| ЦЕЙ |
| ЦЕК |
| ЦЕЛ |
| ЦЕМ |
| ЦЕН |
| ЦЕО |
| ЦЕП |
| ЦЕР |
| ЦЕС |
| ЦЕТ |
| ЦЕФ |
| ЦЕХ |
| ЦЕЦ |
| ЦЕШ |
Целая функция, функция, аналитическая во всей плоскости комплексного переменного (см. Аналитические функции). Примерами Целая функция могут служить алгебраический многочлен a0 + a1z +... + anzn, функции sinz, cosz, ez. Бесконечно удалённая точка является, вообще говоря, изолированной особой точкой Целая функция Для того чтобы бесконечно удалённая точка была устранимой особой точкой (соответственно полюсом), для Целая функция f (z) необходимо и достаточно, чтобы f (z) была постоянна (соответственно была алгебраическим многочленом). Если точка z = ¥ является существенно особой точкой для Целая функция f (z), то f (z) называют трансцендентной Целая функция Таковы, например, функции sinz, cosz, ez.
Для того чтобы f (z) была Целая функция, необходимо и достаточно, чтобы по крайней мере для одной точки z0 имело место соотношение 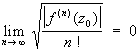
В этом случае разложение f (z) в ряд Тейлора 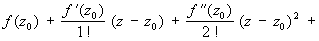
будет сходиться по всей плоскости комплексного переменного.
Основой для классификации трансцендентных Целая функция служит скорость роста М (r) функции, определяемой равенством 
Величину 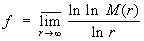
называют порядком Целая функция f (z). В трудах А. Пуанкаре, Ж. Адамара и Э. Бореля была установлена связь между порядком Целая функция и распределением её нулей.
Лит.: Маркушевич А. И., Целые функции, М., 1965.
|
Так же Вы можете узнать о... Эритродермия (от греч. erythros — красный и derma — кожа), группа заболеваний человека, проявляющихся главным образом воспалительной реакцией всего кожного покрова (краснота, отечность, шелушение, зуд). Ад хок (ad hoc — с этой целью, для этой цели), латинский термин, употребляемый в международном праве в отношении органов, создаваемых для выполнения определённых (обычно временных) функций. Анион (от греч. ana — вверх и ion — идущий), отрицательно заряженный ион; в электрическом поле движется к положительному электроду — аноду. Баб-эль-Мандебский пролив [араб. Баб-эль-Мандеб, буквально — ворота скорби (в связи с опасностью плавания)], пролив между юго-западной оконечностью Аравийского полуострова и Африкой. Берсео Гонсало де Берсео (Вегсео) Гонсало де (родился конец 12 в. Брыль Янка (Иван Антонович) [р. 22.7(4.8).1917, Одесса], белорусский советский писатель. Верхнеединск, до 1934 название г. Улан-Удэ — столицы Бурятской АССР. Всемирные фестивали молодёжи и студентов, традиционные массовые международные праздники представителей молодёжи и студентов, борющихся за мир, независимость народов, демократию и социальный прогресс. Германская Демократическая Республика *Население по предварительным данным переписи 1971. Графит (нем. Graphit, от греч. grapho — пишу), минерал, гексагональная кристаллическая модификация чистого углерода, наиболее устойчивая в условиях земной коры. Деснос Робер Деснос (Desnos) Робер (4.7.1900, Париж, — 8. Дурново Петр Николаевич Дурново Пётр Николаевич [1845, Московская губерния, — 11(24). Земельная рента, в эксплуататорских общественно-экономических формациях часть прибавочного продукта, создаваемого непосредственными производителями в сельском хозяйстве, присваиваемая собственниками земли; основная часть арендной платы, выплачиваемой земельным собственникам арендаторами земли. Ионная проводимость в биологических системах обусловлена главным образом диффузией ионов играет важную роль в транспорте веществ между отдельными клеточными структурами, в генерировании и проведении биоэлектрических импульсов и создании разности потенциалов как между отдельными органеллами клетки, так и между её наружной и внутренней средой. |
|