Особая точка
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ОСА |
| ОСБ |
| ОСВ |
| ОСЕ |
| ОСЁ |
| ОСИ |
| ОСК |
| ОСЛ |
| ОСМ |
| ОСН |
| ОСО |
| ОСП |
| ОСС |
| ОСТ |
| ОСУ |
| ОСФ |
| ОСЦ |
| ОСЫ |
| ОСЬ |
| ОСЯ |
Особая точка в математике.
1) Особая точка кривой, заданной уравнением F (x, у) = 0, — точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: 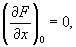
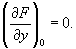
Если при этом не все вторые частные производные функции F (x, у) в точке М0 равны нулю, то Особая точка называют двойной. Если наряду с обращением в нуль первых производных в точке М0 обращаются в нуль и все вторые производные, но не все третьи производные равны нулю, то Особая точка называется тройной, и т.д. При исследовании строения кривой вблизи двойной Особая точка важную роль играет знак выражения 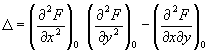

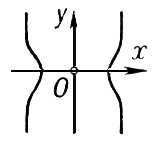
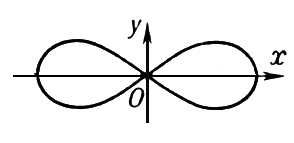
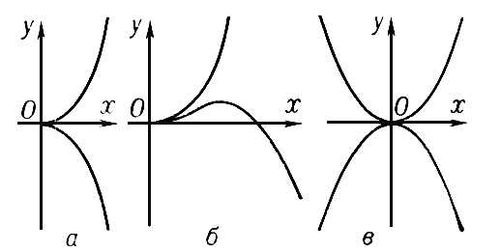
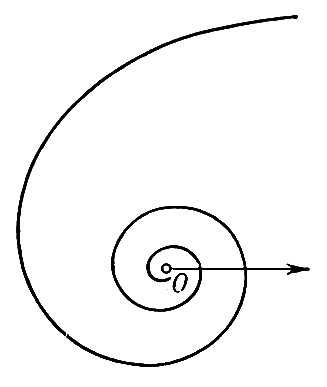
Если D > 0, то Особая точка называется изолированной; например, у кривой у 2 — х 4 + 4x 2 = 0 начало координат есть изолированная Особая точка (см. рис. 1). Если D < 0, то Особая точка называется узловой, или точкой самопересечения; например, у кривой (x 2 + y 2 + a2)2 — 4a 2x 2 — a 4= 0 начало координат есть узловая Особая точка (см. рис. 2). Если D = 0, то О. т. кривой является либо изолированной, либо характеризуется тем, что различные ветви кривой имеют в этой точке общую касательную, например: а) точка возврата 1-го рода — различные ветви кривой расположены по разные стороны от общей касательной и образуют остриё, как у кривой у 2 — х 3 = 0 (см. рис. 3, a); б) точка возврата 2-го рода — различные ветви кривой расположены по одну сторону от общей касательной, как у кривой (у — x 2)2 — х 5 = 0 (см. рис. 3, б); в) точка самоприкосновения (для кривой у 2 — х 4 = 0 начало координат является точкой самоприкосновения; (см. рис. 3, в). Наряду с указанными Особая точка имеется много других Особая точка со специальными названиями; например, асимптотическая точка — вершина спирали с бесконечным числом витков (см. рис. 4), точка прекращения, угловая точка и т.д.
Рис. 1 к ст. Особая точка.
Рис. 2 к ст. Особая точка.
Рис. 3 к ст. Особая точка.
Рис. 4 к ст. Особая точка.
Лит. см. при ст. Дифференциальная геометрия.
2) Особая точка дифференциального уравнения — точка, в которой одновременно обращаются в нуль и числитель и знаменатель правой части дифференциального уравнения  , (1)
, (1)
где Р и Q — непрерывно дифференцируемые функции. Предполагая Особая точка расположенной в начале координат и используя Тейлора формулу, можно представить уравнение (1) в виде 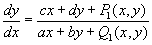 ,
,
где P1(x, у) и Q1(x, у)— бесконечно малые по отношению к 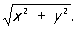 Характер поведения интегральных кривых около Особая точка зависит от корней l1 и l2 характеристического уравнения
Характер поведения интегральных кривых около Особая точка зависит от корней l1 и l2 характеристического уравнения 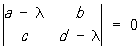 .
.
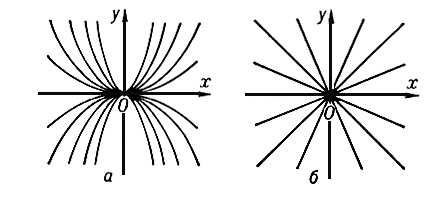
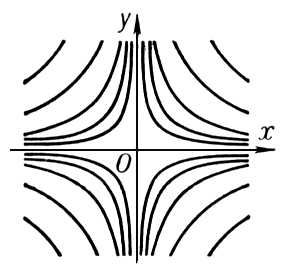
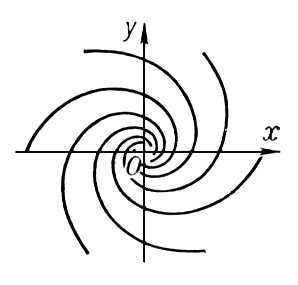
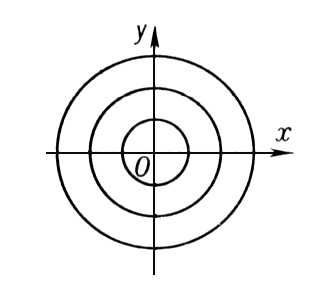
Именно, если l1¹l2 и l1l2 > 0 или l1 = l2, то Особая точка есть узел; все интегральные кривые, проходящие через точки достаточно малой окрестности узла, входят в него. Если l1¹l2 и l1l2 < 0, то Особая точка есть седло; в окрестности седла четыре интегральные кривые (сепаратрисы) входят в Особая точка, а между ними располагаются интегральные кривые типа гипербол. Если l1,2 = a ± i b, a¹ 0 и b¹ 0, то Особая точка есть фокус; все интегральные кривые, проходящие через точки достаточно малой окрестности фокуса, представляют собой спирали с бесконечным числом витков в любой сколь угодно малой окрестности фокуса. Если, наконец, l1,2 = ± ib, b¹ 0, то характер Особая точка не определяется одними линейными членами в разложениях Р (х, у) и Q (x, у), как это имело место во всех перечисленных случаях; здесь Особая точка может быть фокусом или центром, а может иметь и более сложный характер. В окрестности центра все интегральные кривые являются замкнутыми и содержат центр внутри себя. Так, например, точка (0, 0) является узлом для уравнений у ' = 2у/х (l1 = 1, l2 = 2; см. рис. 5, а) и y ' = у/х (l1 = l2 = 1; см. рис. 5, б), седлом для уравнения у' = —у/х (l1 = —1, l2 = 1; см. рис. 6), фокусом для уравнения у' = (х + у) / (х — у) (l1 = 1 — i, l2 = 1 + i; см. рис. 7) и центром для уравнения у' = —x / y (l1 = —i, l2 = i; см. рис. 8).
Рис. 5 к ст. Особая точка.
Рис. 6 к ст. Особая точка.
Рис. 7 к ст. Особая точка.
Рис. 8 к ст. Особая точка.
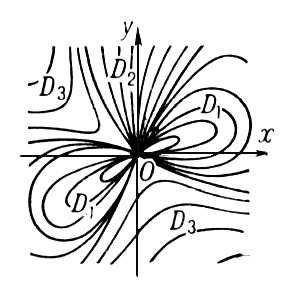
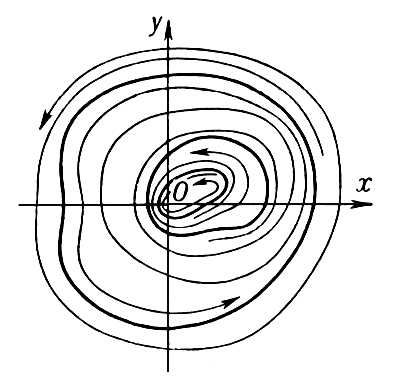
Если 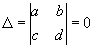 , то Особая точка называют особой точкой высшего порядка. Особая точка высшего порядка могут принадлежать к указанным типам, но могут иметь и более сложный характер. В случае, когда функции Р (х, у) и Q (х, у) аналитические, окрестность Особая точка высшего порядка может распадаться на области: D1 — заполненные интегральными кривыми, обоими концами входящими в Особая точка (эллиптические области), D2 — заполненные интегральными кривыми, одним концом входящими в Особая точка (параболические области), и D3 — области, ограниченные двумя интегральными кривыми, входящими в Особая точка, между которыми расположены интегральные кривые типа гипербол (гиперболические области) (см. рис. 9). Если нет интегральных кривых, входящих в Особая точка, то Особая точка называется точкой устойчивого типа. Окрестность устойчивой Особая точка состоит из замкнутых интегральных кривых, содержащих Особая точка внутри себя, между которыми расположены спирали (см. рис. 10).
, то Особая точка называют особой точкой высшего порядка. Особая точка высшего порядка могут принадлежать к указанным типам, но могут иметь и более сложный характер. В случае, когда функции Р (х, у) и Q (х, у) аналитические, окрестность Особая точка высшего порядка может распадаться на области: D1 — заполненные интегральными кривыми, обоими концами входящими в Особая точка (эллиптические области), D2 — заполненные интегральными кривыми, одним концом входящими в Особая точка (параболические области), и D3 — области, ограниченные двумя интегральными кривыми, входящими в Особая точка, между которыми расположены интегральные кривые типа гипербол (гиперболические области) (см. рис. 9). Если нет интегральных кривых, входящих в Особая точка, то Особая точка называется точкой устойчивого типа. Окрестность устойчивой Особая точка состоит из замкнутых интегральных кривых, содержащих Особая точка внутри себя, между которыми расположены спирали (см. рис. 10).
Рис. 9 к ст. Особая точка.
Рис. 10 к ст. Особая точка.
Изучение Особая точка дифференциальных уравнений, т. е. по существу изучение поведения семейств интегральных кривых в окрестности Особая точка, составляет один из разделов качественной теории дифференциальных уравнений и играет важную роль в приложениях, в частности в вопросах устойчивости движения (работы А. М. Ляпунова, А. Пуанкаре и др.).
Лит. см. при ст. Дифференциальные уравнения.
3) Особая точка однозначной аналитической функции — точка, в которой нарушается аналитичность функции (см. Аналитические функции). Если существует окрестность Особая точка a, свободная от других Особая точка, то точку а называют изолированной Особая точка Если а — изолированная Особая точка и существует конечный 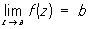 , то a называют устранимой Особая точка Путём надлежащего изменения определения функции в точке а (или доопределения её в этой точке, если функция в ней вообще не определена), именно, полагая f (a) = b, можно добиться того, что a станет обыкновенной точкой исправленной функции. Например, точка z = 0 является устранимой Особая точка для функции
, то a называют устранимой Особая точка Путём надлежащего изменения определения функции в точке а (или доопределения её в этой точке, если функция в ней вообще не определена), именно, полагая f (a) = b, можно добиться того, что a станет обыкновенной точкой исправленной функции. Например, точка z = 0 является устранимой Особая точка для функции 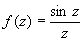 , так как
, так как  ; для функции f 1(z) = f (z), если z¹ 0, и f1(0), = 1, точка z = 0 является обыкновенной точкой [f 1(z) аналитична в точке z = 0]. Если а — изолированная Особая точка и
; для функции f 1(z) = f (z), если z¹ 0, и f1(0), = 1, точка z = 0 является обыкновенной точкой [f 1(z) аналитична в точке z = 0]. Если а — изолированная Особая точка и 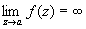 , то а называют полюсом или несущественно особой точкой функции f (z), если же
, то а называют полюсом или несущественно особой точкой функции f (z), если же 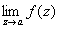 не существует, то существенно особой точкой. Ряд Лорана (см. Лорана ряд) функции f (z) в окрестности изолированной Особая точка не содержит отрицательных степеней z — а, если а — устранимая Особая точка, содержит конечное число отрицательных степеней z — а, если а — полюс (при этом порядок полюса р определяется как наивысшая степень
не существует, то существенно особой точкой. Ряд Лорана (см. Лорана ряд) функции f (z) в окрестности изолированной Особая точка не содержит отрицательных степеней z — а, если а — устранимая Особая точка, содержит конечное число отрицательных степеней z — а, если а — полюс (при этом порядок полюса р определяется как наивысшая степень  , встречающаяся в ряде Лорана), и содержит как угодно высокие степени
, встречающаяся в ряде Лорана), и содержит как угодно высокие степени 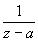 , если а — существенно особая точка. Например, для функции
, если а — существенно особая точка. Например, для функции 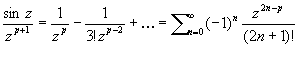 (p = 2, 3, …)
(p = 2, 3, …)
точка z = 0 является полюсом порядка р, для функции 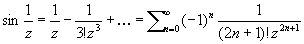
точка z = 0 является существенно особой точкой.
На границе круга сходимости степенного ряда должна находиться по крайней мере одна Особая точка функции, представляемой внутри этого круга данным степенным рядом. Все граничные точки области существования однозначной аналитической функции (естественной границы) являются Особая точка этой функции. Так, все точки единичного круга | z | = 1 являются особыми для функции 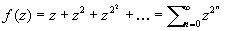 .
.
Для многозначной аналитической функции понятие «Особая точка» более сложно. Помимо Особая точка, в отдельных листах римановой поверхности функции (то есть Особая точка однозначных аналитических элементов) всякая точка ветвления также является Особая точка функции. Изолированные точки ветвления римановой поверхности (то есть такие точки ветвления, что в некоторой их окрестности ни в одном листе нет других Особая точка функции) классифицируются следующим образом. Если а — изолированная точка ветвления конечного порядка и существует конечный 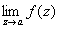 , то Особая точка называют обыкновенной критической точкой; если же
, то Особая точка называют обыкновенной критической точкой; если же 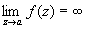 , то а называют критическим полюсом. Если а — изолированная точка ветвления бесконечного порядка и
, то а называют критическим полюсом. Если а — изолированная точка ветвления бесконечного порядка и 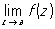 существует (конечный или бесконечный), то а называют трансцендентной Особая точка Все остальные изолированные точки ветвления называют критическими существенно особыми точками. Примеры: точка z = 0 является обыкновенной критической точкой функции
существует (конечный или бесконечный), то а называют трансцендентной Особая точка Все остальные изолированные точки ветвления называют критическими существенно особыми точками. Примеры: точка z = 0 является обыкновенной критической точкой функции 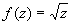 , критическим полюсом функции
, критическим полюсом функции 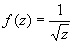 , трансцендентной Особая точка функции f (z) = ln z и критической существенно особой точкой функции f (z) = sin ln z.
, трансцендентной Особая точка функции f (z) = ln z и критической существенно особой точкой функции f (z) = sin ln z.
Всякая Особая точка, кроме устранимой, является препятствием при аналитическом продолжении, т. е. аналитическое продолжение вдоль кривой, проходящей через неустранимую Особая точка, невозможно.
Лит. см. при ст. Аналитические функции.
|
Так же Вы можете узнать о... Интерстициальные клетки (от лат. interstitium — промежуток), межуточные клетки, клетки, расположенные в строме яичников и между канальцами семенников у млекопитающих. Клеёные конструкции, конструкции, состоящие из элементов, образованных склеиванием и сопрягаемых между собой с помощью клеевых соединений или соединений др. Купля-продажа, в гражданском праве один из наиболее распространённых видов договоров, согласно которому продавец обязуется передать имущество в собственность покупателя, а покупатель — принять это имущество и уплатить за него установленную цену. Мальцев Анатолий Иванович [14(27). 11.1909, ныне посёлок Мишеронский Шатурского района Московской области, — 7. Мулинхэ, река на северо-востоке Китая, левый приток р. Оптимальное планирование, см. Планирование оптимальное. Подорлики, крикуны, два близких вида птиц семейства ястребиных; большой П. Рез, в Древней Руси прибыль, процент от денег, данных взаймы. Сиаманги, род обезьян семейства гиббонов. Суммирования блок, суммирующее устройство, аналоговое вычислительное устройство, на выходе которого образуется величина, пропорциональная сумме входных величин (сигналов). У Чэн-энь (1500, провинция Цзянсу, – 1582), китайский писатель. Химическое оружие, отравляющие вещества и средства их боевого применения (ракеты, артиллерийские снаряды, мины, авиационные бомбы, химические фугасы, ручные химические гранаты, ядовито-дымные шашки). Шумерля, город (с 1937) республиканского (АССР) подчинения, центр Шумерлинского района Чувашской АССР. Активизация тектоническая, переход отдельных участков земной коры в более подвижное состояние в связи с увеличением интенсивности вертикальных движений земной коры. Барлах Эрнст Барлах (Barlach) Эрнст (2.1.1870, Ведель, Шлезвиг-Гольштейн, — 24. Валовая продукция промышленного предприятия, объём продукции, произведённой на промышленном предприятии за определённый период, в денежном измерении. Гарсиа Эрнандес Анхель Гарсиа Эрнандес (García Hernández) Анхель (1900—14. Двур-Кралове (Dvur Kralove nad Labern), город в Чехословакии, в Чешской Социалистической Республике на р. Заочное образование, одна из форм подготовки и повышения квалификации специалистов с высшим и средним специальным образованием, а также получения общего среднего образования без отрыва от работы на производстве. |
|