Эллиптические функции
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ЭЛА |
| ЭЛВ |
| ЭЛГ |
| ЭЛД |
| ЭЛЕ |
| ЭЛИ |
| ЭЛК |
| ЭЛЛ |
| ЭЛМ |
| ЭЛО |
| ЭЛП |
| ЭЛС |
| ЭЛУ |
| ЭЛЬ |
| ЭЛЮ |
| ЭЛЯ |
Эллиптические функции, функции, связанные с обращением эллиптических интегралов. Эллиптические функции применяются во многих разделах математики и механики как при теоретических исследованиях, так и для численных расчётов.
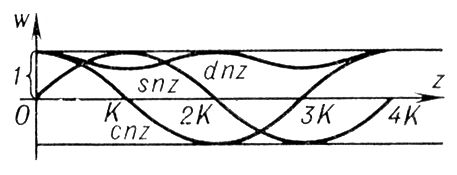
Рис. к ст. Эллиптические функции.
Подобно тому как тригонометрическая функция u = sinx является обратной по отношению к интегралу 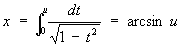
так обращение нормальных эллиптических интегралов 1-го рода 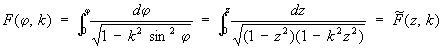
где z = sinjw, k — модуль эллиптического интеграла, порождает функции: j = am z — амплитуда z (эта функция не является Эллиптические функции) и w = sn z = sin (am z) — синус амплитуды. Функции cn — косинус амплитуды и dn z — дельта амплитуды определяются формулами 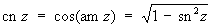
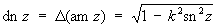
Функции sn z, cn z, dn z называют Э. ф. Якоби. Они связаны соотношением
sn2z + cn2z = k2sn2z + dn2z = 1.
На рис. представлен вид графиков Э. ф. Якоби. Они связаны соотношением
sn2z + cn2z = k2sn2z + dn2z = 1
На рис. представлен вид графиков Э. ф. Якоби для действительного x и 0 < k < 1; а 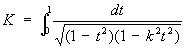
— полный нормальный эллиптический интеграл 1-го рода и 4K — основной период Эллиптические функции sn z. В отличие от однопериодической функции sin х, функция sn z — двоякопериодическая. Её второй основной период равен 2iK, где 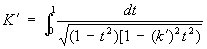
и 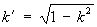 — дополнительный модуль. Периоды, нули и полюсы Э. ф. Якоби приведены в таблице, где m и n — любые целые числа.
— дополнительный модуль. Периоды, нули и полюсы Э. ф. Якоби приведены в таблице, где m и n — любые целые числа.
|
Функции |
Периоды |
Нули |
Полюсы |
|
sn z |
4Km + 2iK'n |
2mK + 2iK'n |
}2mK + (2n + 1) iK' |
|
cn z |
4K + (2K + 2iK') n |
(2m + 1) K + 2iK'n | |
|
dn z |
2Km + 4iK'n |
(2m + 1) K + (2n + 1) iK |
Эллиптические функции Вейерштрасса Ã(х) может быть определена как обратная нормальному эллиптическому интегралу Вейерштрасса 1-го рода 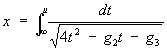
где параметры g2 и g2 — называются инвариантами Ã(x). При этом предполагается, что нули e1, e2 и e3 многочлена 4t3 — g2t — g3 различны между собой (в противном случае интеграл (*) выражался бы через элементарные функции). Эллиптические функции Вейерштрасса Ã(х) связана с Э. ф. Якоби следующими соотношениями: 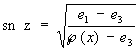 ,
, 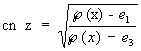 ,
,
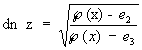 .
.
Любая мероморфная двоякопериодическая функция f (z) с периодами w1 и w2, отношение которых мнимо, т. е. f (z + mw1 + пw2) = f (z) при m, n = 0, ±1, ±2,... и 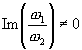 , является Эллиптические функции Для построения Эллиптические функции, а также численных расчётов применяют сигма-функции и тэта-функции.
, является Эллиптические функции Для построения Эллиптические функции, а также численных расчётов применяют сигма-функции и тэта-функции.
Изучению Эллиптические функции предшествовало накопление знаний об эллиптических интегралах, систематическое изложение теории которых дал А. Лежандр. Основоположниками теории Эллиптические функции являются Н. Абель (1827) и К. Якоби (1829). Последний дал развёрнутое изложение теории Эллиптические функции, названное его именем. В 1847 Ж. Лиувилль опубликовал изложение основ общей теории Эллиптические функции, рассматриваемых как мероморфные двоякопериодические функции. Представление Эллиптические функции через Ã-функцию, а также z-, s-функции дано К. Вейерштрассом в 40-х гг. 19 в. (две последние не являются Эллиптические функции).
Лит.: Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968; Уиттекер Э, Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Эллиптические и автоморфные функции. Функции Ламе и Матье, пер. с англ., М., 1967.
|
Так же Вы можете узнать о... Кальвино Итало Кальвино (Calvino) Итало (р. 15.10.1923, Сантьяго-де-лас-Вегас, Куба), итальянский писатель. Окарина (итал. ocarina, буквально — гусёнок), духовой музыкальный инструмент со свистковым устройством. Тепловой баланс моря, соотношение прихода и расхода теплоты в море, основными составляющими которого являются: радиационный баланс, турбулентный и конвективный теплообмен моря с атмосферой, потеря теплоты на испарение, перенос её течениями. Балуба, луба, народ в Демократической Республике Конго (столица Киншаса), живут преимущественно в провинции Катанга и сопредельных районах провинции Касаи. Импульстерапия (от лат. impulsus — удар, толчок и терапия), применение с лечебной целью различных физических воздействий (электрический ток, ультраи сверхвысокочастотные колебания электромагнитного поля, ультразвук, механическое давление, свет и др. Нетканых текстильных материалов институт Всесоюзный научно-исследовательский (ВНИИНТМ), в ведении министерства лёгкой промышленности СССР. Судебная власть, в буржуазном государственном и конституционном праве — система органов, на которые законом возлагается осуществление правосудия. Арбес Якуб Арбес (Arbes) Якуб (12.6.1840, Прага, — 8.4. Западноевропейский союз, военно-политическая организация в составе Бельгии, Великобритании, Италии, Люксембурга, Нидерландов, Франции, ФРГ. Музейный фонд СССР, совокупность памятников естественной истории, материальной и духовной культуры в стране (независимо от времени их происхождения, места нахождения, материала и техники изготовления), имеющих научное, политическое, историческое или художественное значение. Сосущие инфузории (Suctoria) подкласс простейших класса инфузории. Албанская партия труда (АПТ; Partia е Punes е Shqiperise) (до 1948 — Коммунистическая партия Албании; КПА), основана 8 ноября 1941 в Тиране в условиях оккупации Албании итальянскими фашистами; создана в результате объединения отдельных коммунистических групп (гг. Дреш Жан Дреш (Dresch) Жан (р. 30.11.1905, Париж), французский географ и геоморфолог, профессор (1931). Микробиологическая техника, совокупность методов и аппаратуры для изучения микроорганизмов в лабораторных условиях. Симода Сёдзи (р. 5.9.1913, о. Окинава), японский писатель. Яковлев Борис Николаевич [5(17).9.1890, Москва, — 8. Деперсонализация (от де... и лат. persona — личность, лицо), расстройство самосознания, чувство изменения своего «я». Маркиш Перец Давидович [25.11(7.12).1895 — 12. |
|