Квадратичное отклонение
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| КВА |
| КВЕ |
| КВИ |
| КВО |
| КВЯ |
Квадратичное отклонение, квадратичное уклонение, стандартное отклонение величин x1, x2,..., xn от а — квадратный корень из выражения 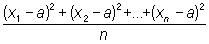 .
.
Наименьшее значение Квадратичное отклонение имеет при а = 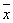 , где
, где 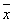 — среднее арифметическое величин x1, x2,..., xn:
— среднее арифметическое величин x1, x2,..., xn: 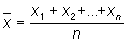 .
.
В этом случае Квадратичное отклонение может служить мерой рассеяния системы величин x1, x2,..., xn. Употребляют также более общее понятие взвешенного Квадратичное отклонение 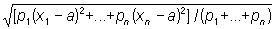 ;
;
числа p1,..., pn называют при этом весами, соответствующими величинам x1,..., xn. Взвешенное Квадратичное отклонение достигает наименьшего значения при а, равном взвешенному среднему: (p1x1 +... + pnxn)/(p1 +...+ pn).
В теории вероятностей Квадратичное отклонение ох случайной величины Х (от её математического ожидания) называют квадратный корень из дисперсии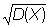 .
.
Квадратичное отклонение употребляют как меру качества статистических оценок и называют в этом случае квадратичной ошибкой. См. Ошибок теория.
|
Так же Вы можете узнать о... Валлер Макс Валлер (Waller) Макс [также Зибель (Siebel) — псевдонимы; настоящая фамилия и имя Варломон (Warlomont) Морис] (24. Вермер Ян Вермер Делфтский (Vermeer van Delft) Ян (крещён 31. Вихерт Эрнст Вихерт (Wiechert) Эрнст (18.5.1887, Форстхауз, — 24. Восков Семён Петрович Восков Семён (настоящее имя Самуил) Петрович (1889, с. Газопровод магистральный, сооружение для транспортировки на большие расстояния (сотни и тысячи км) горючих газов от места их добычи или производства к пунктам потребления. Гемоглобинурия (от гемоглобин и греч. uron — моча), появление гемоглобина в моче. Гиперболоидная передача, зубчатая передача для осуществления вращения между произвольно расположенными, не лежащими в одной плоскости осями, при постоянном передаточном числе. Горки, город, центр Горецкого района Могилёвской области БССР, на р. Грузинское письмо, самостоятельная система письма, обслуживающая грузинский язык. Двойникование, образование в монокристалле областей с закономерно измененной ориентацией кристаллической структуры. Джанелидзе Иустин Ивлианович (Юстин Юлианович) [20. Добрович Никола Добрович (Dobrović) Никола (12. Дыгат Станислав Дыгат (Dygat) Станислав (р. 5.12.1914, Варшава), польский писатель. |
|