Ошибок теория
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ОША |
| ОШЕ |
| ОШИ |
| ОШК |
| ОШМ |
| ОШО |
| ОШС |
Ошибок теория, раздел математической статистики, посвященный построению уточнённых выводов о численных значениях приближённо измеренных величин, а также об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, так как каждое измерение содержит некоторую ошибку. Различают 3 основных вида ошибок: систематические, грубые и случайные. Систематические ошибки всё время либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на измерения и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики (см. Наблюдений обработка). Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредвиденным образом то в сторону уменьшения, то в сторону увеличения результатов.
Ошибок теория занимается изучением лишь грубых и случайных ошибок. Основные задачи Ошибок теория: разыскание законов распределения случайных ошибок, разыскание оценок (см. Статистические оценки) неизвестных измеряемых величин по результатам измерений, установление погрешностей таких оценок и устранение грубых ошибок.
Пусть в результате n независимых равноточных измерений некоторой неизвестной величины а получены значения x1, x2,..., xn. Разности
d1 = x1 — a,…, dn = xn — a
называются истинными ошибками. В терминах вероятностной Ошибок теория все di трактуются как случайные величины; независимость измерений понимается как взаимная независимость случайных величин d1,..., dn. Равноточность измерений в широком смысле истолковывается как одинаковая распределённость: истинные ошибки равноточных измерений суть одинаково распределённые случайные величины. При этом математическое ожидание случайных ошибок b = Ed1 =...= Еdn называется систематической ошибкой, а разности d1— b,...,dn— b — случайными ошибками. Таким образом, отсутствие систематической ошибки означает, что b = 0, и в этой ситуации d1,..., dn суть случайные ошибки. Величину 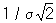 , где а — квадратичное отклонение, называют мерой точности (при наличии систематической ошибки мера точности выражается отношением
, где а — квадратичное отклонение, называют мерой точности (при наличии систематической ошибки мера точности выражается отношением 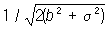 . Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений
. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений
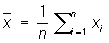 ,
,
а разности D1 = x1— 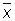 ,..., Dn = xn —
,..., Dn = xn — 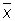 называются кажущимися ошибками. Выбор
называются кажущимися ошибками. Выбор 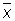 в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка
в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка 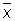 с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон); оценка
с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон); оценка 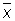 лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
D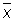 = E(
= E(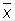 — а)2 = s2/n.
— а)2 = s2/n.
Опыт показывает, что практически очень часто случайные ошибки di подчиняются распределениям, близким к нормальному (причины этого вскрыты так называемыми предельными теоремами теории вероятностей). В этом случае величина 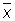 имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s2/n. Если распределения di в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы, не меньше D
имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s2/n. Если распределения di в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы, не меньше D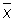 . Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
. Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
Если дисперсия s2 отдельных измерений заранее известна, то для её оценки пользуются величиной
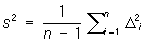
(Es2 = s2, т. е. s2 — несмещенная оценка для s2), если случайные ошибки di имеют нормальное распределение, то отношение
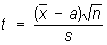
подчиняется Стьюдента распределению с n— 1 степенями свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства а »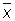 (см. Наименьших квадратов метод).
(см. Наименьших квадратов метод).
Величина (n — 1) s2/s2 при тех же предположениях имеет распределение c2 (см. «Хи-квадрат»распределение) с n— 1 степенями свободы. Это позволяет оценить погрешность приближённого равенства s»s. Можно показать, что относительная погрешность |s — s|Is не будет превышать числа q с вероятностью
w = F (z2, n — 1) — F (z1, n — 1),
где F (z, n — 1) — функция распределения c2,
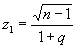 ,
, 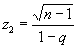 .
.
Лит.: Линник Ю. В., Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, 2 изд., М., 1962; Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968.
Л. Н. Большев.
|
Так же Вы можете узнать о... Эпидемический очаг, применяемое в эпидемиологии понятие, охватывающее место пребывания источника возбудителя инфекции (больного или бактерионосителя) с прилегающей территорией в пределах существующей опасности передачи заразного начала окружающим. Арнон Даниел Исраэл Арнон (Arnon) Даниел Исраэл (р. 14.11.1910), американский биохимик и физиолог растений. Бруевич Николай Григорьевич [р. 31.10(12.11). Гамелен Морис Гюстав Гамелен (Gamelin) Морис Гюстав (20.9.1872, Париж, — 18. Дерматин, гранитоль, вид искусственной кожи из ткани с нитроцеллюлозным покрытием (плёнкой). «Известия Министерства иностранных дел», журнал, издававшийся в Петрограде в 1912—17 под редакцией барона Б. Классификация языков, 1) генетическая К. я. — по признаку родства, т. Ланглей Сэмюэл Ланглей (Langley) Сэмюэл (1834—1906), американский астроном; см. Менгс Антон Рафаэль Менгс (Mengs) Антон Рафаэль (22.3.1728, Ауссиг, ныне Усти на Лабе, Чехословакия, — 29. Новороссийские цементные заводы, цементные заводы комбината Новоросцемент; расположены в Новороссийске и на ж. Пинены (от лат. pinus — сосна), бициклические терпены C10H16; бесцветные жидкости с запахом хвои сосны, хорошо растворимые в неполярных органических растворителях, нерастворимы в воде; на воздухе (особенно на свету) легко окисляются. Регистр (в вычислит. технике) Регистр ЦВМ, часть памяти вычислительной машины обычно ёмкостью в одно машинное слово, предназначенная для запоминания (а иногда также и для преобразования) кодов. Сквален (от лат. squalus — акула), ациклический полиненасыщенный жидкий углеводород состава C30H50 с tkип 242 °С, растворимый во многих органических растворителях. Тендер (англ. tender, от tend — обслуживать), 1) обычно прицепленная к паровозу трёх-, четырёх-, шестиосная повозка с запасами воды и топлива. Флинт Ричард Фостер Флинт (Flint) Ричард Фостер (1.3.1902, Чикаго, – 6. Швырялка, машина для подкапывания рядков картофеля, отделения клубней от почвы и ботвы и разбрасывания клубней по полю. Аквитанская низменность, низменность во Франции, то же, что Гароннская низменность. Белозубки (Crocidura), род млекопитающих семейства землероек отряда насекомоядных. «Вильнис» («Vilnis» — «Волна»), рабочая социал-демократическая газета. |
|