Нормированное кольцо
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| НОА |
| НОБ |
| НОВ |
| НОГ |
| НОД |
| НОЕ |
| НОЖ |
| НОЗ |
| НОИ |
| НОЙ |
| НОК |
| НОЛ |
| НОМ |
| НОН |
| НОО |
| НОП |
| НОР |
| НОС |
| НОТ |
| НОУ |
| НОЧ |
| НОЯ |
Нормированное кольцо, важное понятие функционального анализа, значительно расширившее область его приложений. Элементы Нормированное кольцо являются одновременно и точками некоторого геометрического образования — полного нормированного пространства, и элементами некоторого алгебраического образования — кольца, в котором определено ещё умножение на числа (причём алгебраические операции непрерывны по норме). Примерами Нормированное кольцо могут служить: кольцо С всех непрерывных функций на отрезке [0,1] с обычными алгебраическими операциями и нормой 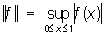 , кольцо L1 всех абсолютно интегрируемых на прямой функций, в котором умножение определено как свёртывание:
, кольцо L1 всех абсолютно интегрируемых на прямой функций, в котором умножение определено как свёртывание:
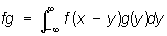 ,
, 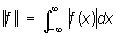 ;
;
кольцо матриц n-го порядка; кольцо ограниченных операторов гильбертова пространства — кольцо операторов, и т.д. Наиболее разработана теория коммутативных Нормированное кольцо (т. е. Нормированное кольцо, в которых умножение перестановочно: ху = ух), созданная И. М. Гельфандом.
Наряду с термином «Нормированное кольцо» употребляется термин «банахова алгебра».
Лит.: Наймарк М. А., Нормированные кольца, М., 1956.
|
Так же Вы можете узнать о... Польский государственный театр оперы и балета («Театр Вельки», Teatr Wielki), старейший музыкальный театр в Польше. Ревизионный порядок, по советскому праву принцип рассмотрения гражданских и уголовных дел в кассационной инстанции (см. Северный морской канал, Нордзе-канал (Noordzee Kanaal), судоходный канал в Нидерландах. Спик Джон Хеннинг Спик (Speke) Джон Хеннинг (4.5.1827, Джорданс, Сомерсетшир, — 15. Териодонты, подотряд вымерших пресмыкающихся подкласса зверообразных; то же, что зверозубые. Уставобранители [серб.-хорв. – защитники устава (т. Ходжа Энвер Ходжа (Hoxha) Энвер (родился 16.10.1908, Гирокастра), государственный и политический деятель Албании. Шкворень, стержень шарнира поворотного соединения частей транспортных машин. Абак (греч. ábax, abákion, латинский abacus — доска, счётная доска), Аржантёй (Argenteuil), город во Франции, в департаменте Сена и Уаза, на р. Бёрк Эдмунд Бёрк (Burke) Эдмунд (12.1.1729, Дублин, — 9. Векшинский Сергей Аркадьевич [р. 15(27).10.1896, Псков], советский учёный, специалист в области электровакуумной техники, академик АН СССР (1953; член-корреспондент 1946), Герой Социалистического Труда (1956). |
|