Кольцо алгебраическое
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| КОА |
| КОБ |
| КОВ |
| КОГ |
| КОД |
| КОЖ |
| КОЗ |
| КОИ |
| КОЙ |
| КОК |
| КОЛ |
| КОМ |
| КОН |
| КОО |
| КОП |
| КОР |
| КОС |
| КОТ |
| КОУ |
| КОФ |
| КОХ |
| КОЦ |
| КОЧ |
| КОШ |
| КОЩ |
| КОЭ |
| КОЮ |
| КОЯ |
Кольцо алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами Кольцо алгебраическое могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных, отрицательных чисел и нуля; 2) множество всех чётных чисел и вообще целых чисел, кратных данному числу n, 3) множество всех рациональных чисел. Общим в этих трёх примерах является то, что сложение и умножение чисел, входящих в систему, не выводят за пределы системы (следует отметить, что и вычитание не выводит за пределы системы). В различных областях математики часто приходится иметь дело с разнообразными множествами (они могут состоять, например, из многочленов или матриц, см. примеры 7 и 9), над элементами которых можно производить две операции, весьма похожие по своим свойствам на сложение и умножение обычных чисел. Предметом теории Кольцо алгебраическое является изучение свойств обширного класса такого рода множеств.
Кольцом называют непустое множество R, для элементов которого определены две операции — сложение и умножение, сопоставляющие любым двум элементам а, b из R, взятым в определённом порядке, один элемент а + b из R — их сумму и один элемент ab из R — их произведение, причём предполагаются выполненными следующие условия (аксиомы Кольцо алгебраическое):
I. Коммутативность сложения:
а+b=b+ а.
II. Ассоциативность сложения:
а + (b + с) = (а + b) + с.
III. Обратимость сложения (возможность вычитания): уравнение а + х = b допускает решение х = b—a.
IV. Дистрибутивность: а (b + с) = ab+ac, (b + с) а = ba + са.
Перечисленные свойства показывают, что элементы Кольцо алгебраическое образуют коммутативную группу относительно сложения. Дальнейшими примерами Кольцо алгебраическое могут служить множества; 4) всех действительных чисел; 5) всех комплексных чисел; 6) комплексных чисел вида a + bi с целыми а, b; 7) многочленов от одного переменного х с рациональными, действительными или комплексными коэффициентами; 8) всех функций, непрерывных на данном отрезке числовой прямой; 9) всех квадратных матриц порядка n с действительными (или комплексными) элементами; 10) всех кватернионов; 11) всех чисел Кэли — Диксона, то есть выражений вида a + bе, где a,b — кватернионы, е — буква; сложение и умножение чисел Кэли — Диксона определяются равенствами (a + bе) + (a1 + b1e) = (a + a1) + (b + b1) e, (a + bе)(a1 + b1e) = (aa1 — b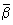 1) + (aa1 + b
1) + (aa1 + b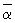 ) e, где
) e, где 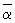 — кватернион, сопряжённый к a; 12) всех симметрических матриц порядка n с действительными элементами относительно операций сложения матриц и «йорданового» умножения а·b =
— кватернион, сопряжённый к a; 12) всех симметрических матриц порядка n с действительными элементами относительно операций сложения матриц и «йорданового» умножения а·b =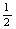 (аb + ba); 13) векторов трёхмерного пространства при обычном сложении и векторном умножении.
(аb + ba); 13) векторов трёхмерного пространства при обычном сложении и векторном умножении.
Во многих случаях на умножение в Кольцо алгебраическое налагаются дополнительные ограничения. Так, если а (bc) = (ab) c, то Кольцо алгебраическое называют ассоциативным (примеры 1—10); если в Кольцо алгебраическое выполняются равенства (aa) b = a (ab), (ab) b = a (bb), то оно называется альтернативным кольцом (пример 11); если в Кольцо алгебраическое выполняются равенства ab = ba, (ab) (аа) = ((аа) b) a, то оно называется йордановым кольцом (пример 12); если в Кольцо алгебраическое выполняются равенства а (bc) + b (ca) + с (аb) = 0, a2 = 0, то оно называется кольцом Ли (пример 13); если ab = ba, то Кольцо алгебраическое называют коммутативным (примеры 1—8, 12). Операции сложения и умножения в Кольцо алгебраическое во многом похожи по своим свойствам на соответствующие операции над числами. Так, элементы Кольцо алгебраическое можно не только складывать, но и вычитать; существует элемент 0 (нуль) с обычными свойствами; для любого элемента а существует противоположный, т. е. такой элемент —а, что а + (—a) = 0; произведение любого элемента на элемент 0 всегда равно нулю. Однако на примерах 8—9, 12—13 можно убедиться, что Кольцо алгебраическое может содержать отличные от нуля элементы а, b, произведение которых равно нулю: ab = 0; такие элементы называют делителями нуля. Ассоциативное коммутативное Кольцо алгебраическое без делителей нуля называют областью целостности (примеры 1—7). Так же, как и в области целых чисел, не во всяком Кольцо алгебраическое возможно деление одного элемента на другой, если же это возможно, то есть если всегда разрешимы уравнения ax = b и уа = b при а¹0, то Кольцо алгебраическое называют телом (примеры 3—5, 10, 11). Ассоциативное коммутативное тело принято называть полем (примеры 3— 5) (см. Поле алгебраическое). Весьма важны для многих отделов алгебры Кольцо алгебраическое многочленов с одним или несколькими переменными над произвольным полем и Кольцо алгебраическое матриц над ассоциативными телами, определяемые аналогично Кольцо алгебраическое примеров 7 и 9. Многие классы Кольцо алгебраическое всё чаще находят приложения и вне алгебры. Важнейшими из них являются: Кольцо алгебраическое функций и Кольцо алгебраическое операторов, сыгравшие большую роль в развитии функционального анализа; альтернативные тела, применяемые в проективной геометрии; так называемые дифференциальные Кольцо алгебраическое и поля, отразившие интересную попытку применить теорию Кольцо алгебраическое к дифференциальным уравнениям.
При изучении Кольцо алгебраическое большое значение имеют те или иные способы сличения друг с другом различных Кольцо алгебраическое Одним из наиболее плодотворных является гомоморфное отображение (гомоморфизм), т. е. такое однозначное отображение R®R' кольца R на кольцо R', что из а ® a', b ®b' следует а + b® a' +b' и ab®a'b'. Если это отображение также и взаимно однозначное, то оно называется изоморфизмом, а кольца R и R' изоморфными. Изоморфные Кольцо алгебраическое обладают одинаковыми алгебраическими свойствами.
Множество М элементов кольца R называют подкольцом, если М само является Кольцо алгебраическое относительно операций, определённых в R. Подкольцо М называют левым (правым или двусторонним) идеалом кольца R, если для любых элементов т из М и r из R произведение rm (соответственно mr или как rm, так и mr) лежит в М. Элементы а и b кольца R называют сравнимыми по идеалу М, если а — b принадлежит М. Всё Кольцо алгебраическое разбивается на классы сравнимых элементов — классы вычетов по идеалу М. Если определить сложение и умножение классов вычетов по двустороннему идеалу М через сложение и умножение элементов этих классов, то сами классы вычетов образуют Кольцо алгебраическое — фактор кольцо R/M кольца R по идеалу М. Имеет место теорема о гомоморфизме Кольцо алгебраическое: если каждому элементу Кольцо алгебраическое поставить в соответствие содержащий его класс, то получают гомоморфное отображение кольца R на факторкольцо RM; обратно, если R гомоморфно отображается на R', то множеством элементов из R, отображающихся в нуль кольца R', будет двусторонним идеалом в R, и R' изоморфно R/M.
Среди различных типов Кольцо алгебраическое легче других поддаются изучению и сравнительно чаще находят приложение так называемые алгебры: кольцо R называют алгеброй над полем Р, если для любых a из Р и r из R определено произведение ar также из R, причём (a + b) r = ar + br, a(r + s)=ar + as, (ab) r = a(br), a(rs) = (ar) s = r (as),er = r для любых a, b из Р и r, s из R, где e — единица поля Р. Если все элементы алгебры линейно выражаются через n линейно независимых элементов (см. Линейная зависимость), то R называют алгеброй конечного ранга n, или гиперкомплексной системой (см. Гиперкомплексные числа). Примерами алгебр могут служить комплексные числа (алгебра ранга 2 над полем действительных чисел), полное Кольцо алгебраическое матриц с элементами из поля Р (которое является алгеброй ранга n2 над Р), Кольцо алгебраическое примера 10 (алгебра ранга 4 над полем действительных чисел), Кольцо алгебраическое примера 8 и др.
Для целых чисел и Кольцо алгебраическое многочленов справедлива теорема об однозначной разложимости элемента в произведение простых, т. с. далее не разложимых элементов. Эта теорема верна для любых Кольцо алгебраическое главных идеалов, то есть областей целостности, в которых любой идеал состоит из кратных одного элемента. Частным случаем таких Кольцо алгебраическое являются евклидовы Кольцо алгебраическое, то есть Кольцо алгебраическое, где любому элементу а ¹ 0 соответствует неотрицательное целое число n (a), причём n (ab) ³n (a) и для любых а и b ¹ 0 существуют такие q и r, что а = bq +r и либо n (r)<n (b), либо r = 0. Таковы, например, Кольцо алгебраическое многочленов и Кольцо алгебраическое примеров 1 и 6. Для широкого класса Кольцо алгебраическое верна теорема об однозначном разложении идеала в произведение простых идеалов, хотя для самих элементов она не выполняется. Основы теории разложения идеалов и абстрактных Кольцо алгебраическое были заложены Э. Нётер (в 20-х гг. 20 в.).
Одним из первых в России теорией Кольцо алгебраическое занимался Е. И. Золотарёв (70-е гг. 19 в.); его исследования относятся к числовым Кольцо алгебраическое, а именно — к теории разложения идеалов в них. В Советском Союзе теория Кольцо алгебраическое разрабатывается в основном в трёх центрах: Москве, Новосибирске и Кишиневе.
Лит.: Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968; Энциклопедия элементарной математики, кн. 1, М. — Л., 1951; Ван-дер-Варден Б. Л., Современная алгебра, пер. с нем., 2 изд., ч. 1—2, М. — Л.,1947; Джекобсон Н., Строение колец, пер. с англ., М., 1961; Ленг С., Алгебра, пер. с англ., М., 1968.
|
Так же Вы можете узнать о... Милиция (от лат. militia — войско), в СССР административно-исполнительный орган государства, призванный обеспечивать охрану общественного порядка, социалистической собственности, прав и законных интересов граждан, предприятий, организаций и учреждений от преступных посягательств и иных антиобщественных действий. Мстиславль, город, центр Мстиславского района Могилёвской области БССР. Неодикумарин, пелентан, лекарственный препарат из группы антикоагулянтов непрямого действия. Общественные издержки производства, см. Издержки производства, Стоимость. Отдельность минералов, способность кристаллов или кристаллических зёрен минералов раскалываться по некоторым более или менее параллельным плоскостям. Перевозчик (Actitis hypoleucos), птица семейства ржанок подотряда куликов. Подгайцы, город в Бережанском районе Тернопольской области УССР, на р. Префект претория (лат. praefectus praetorio), в Древнем Риме, 1) командир преторианцев. Радин Николай Мариусович (настоящая фамилия — Казанков) [3(15). Ричардсон Генри Хендел Ричардсон (Richardson) Генри Хендел (псевдоним; настоящее имя и фамилия Этель Флоренс Линдсей Ричардсон) (3. Сандомежская низменность, Сандомирская котловина (Kotlina Sandomierska), низменность на юго-востоке Польши, в междуречье Вислы и Сана, занимающая часть Предкарпатского прогиба; сложена преимущественно аллювиальными отложениями. Сеута, город на Средиземноморском побережье Марокко, в восточной части Гибралтарского пролива. Сови Альфред Сови(Sauvy) Альфред (р. 31.10.1898, Вильнёв-де-ла-Рао, Восточные Пиренеи), французский социолог, демограф и экономист. Степная фауна, комплекс животных, характерных для степей. Таманской армии поход 1918, героический поход советских войск с Таманского полуострова через Туапсе на соединение с главными силами Красной Армии Северного Кавказа в августе — сентябре 1918. Ток электрический, см. Электрический ток. |
|