Сингулярные интегральные уравнения
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| СИА |
| СИБ |
| СИВ |
| СИГ |
| СИД |
| СИЕ |
| СИЗ |
| СИИ |
| СИЙ |
| СИК |
| СИЛ |
| СИМ |
| СИН |
| СИО |
| СИП |
| СИР |
| СИС |
| СИТ |
| СИУ |
| СИФ |
| СИХ |
| СИЦ |
| СИШ |
| СИЭ |
Сингулярные интегральные уравнения,интегральные уравнения с ядрами, обращающимися в бесконечность в области интегрирования так, что соответствующий несобственный интеграл, содержащий неизвестную функцию, расходится и заменяется своим главным значением по Коши. Примером Сингулярные интегральные уравнения может служить следующее уравнение с т. н. ядром Гильберта:
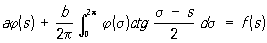
решением которого является функция
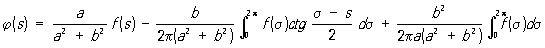 ,
,
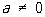 ,
, 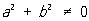 ,
,
где первый интеграл также понимается в смысле главного значения по Коши.
Хорошо изученным общим классом С. и. у. являются уравнения с ядром Коши вида:
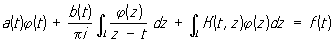 , (*)
, (*)
где a (t), b (t), f (t) — заданные непрерывные функции точки t пути интегрирования L (который может состоять из конечного числа гладких самонепересекающихся замкнутых или незамкнутых кривых с непрерывной кривизной) в комплексной плоскости; сингулярный интеграл
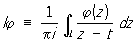
понимается как предел при e® 0 интеграла 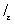 j по пути Le, который получается из L после удаления симметричной относительно точки t дуги длины 2e. Ядро K (t, z) предполагается принадлежащим к одному из тех классов, которые рассматриваются в теории несингулярных интегральных уравнений. К Сингулярные интегральные уравнения вида (*) приводят многие задачи теории аналитических функций, теории упругости, гидродинамики и др.
j по пути Le, который получается из L после удаления симметричной относительно точки t дуги длины 2e. Ядро K (t, z) предполагается принадлежащим к одному из тех классов, которые рассматриваются в теории несингулярных интегральных уравнений. К Сингулярные интегральные уравнения вида (*) приводят многие задачи теории аналитических функций, теории упругости, гидродинамики и др.
Исследование Сингулярные интегральные уравнения (*) опирается на свойства сингулярного интеграла Ij, которые зависят от предположений, делаемых относительно j. Подробно Сингулярные интегральные уравнения исследованы в пространстве непрерывных функций j и в пространстве функций, интегрируемых с квадратом. Основное свойство сингулярного интеграла Ij выражается равенством 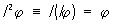 , справедливым для широкого класса функций.
, справедливым для широкого класса функций.
Многие результаты теории Сингулярные интегральные уравнения почти без изменений переносятся на системы Сингулярные интегральные уравнения, которые можно записать в виде (*), если под а и b понимать матричные функции, а под f и j — векторы (одноколонные матрицы). Теория обобщается также на случай системы Сингулярные интегральные уравнения с разрывными коэффициентами и кусочно-гладким путём интегрирования. Изучены также некоторые классы Сингулярные интегральные уравнения в многомерных областях.
Сингулярные интегральные уравнения впервые (начало 20 в.) встретились в исследованиях А. Пуанкаре (по теории приливов) и Д. Гильберта (по краевым задачам). Ряд важных свойств С. и. у. установил нем. математик Ф. Нётер. Для разработки теории Сингулярные интегральные уравнения важное значение имели работы Т. Карлемана и И. И. Привалова. Наиболее полные результаты получены сов. учёными (Н. И. Мусхелишвили, И. Н. Векуа, В. Д. Купрадзе и др.).
Лит.: Мусхелишвили Н. И., Сингулярные интегральные уравнения. Граничные задачи теории функций и некоторые их приложения к математической физике, 3 изд., М., 1968; Векуа Н. П., Системы сингулярных интегральных уравнений и некоторые граничные задачи, 2 изд., М., 1970.
|
Так же Вы можете узнать о... Квантовая химия, область теоретической химии, в которой вопросы строения и реакционной способности химических соединений, химические связи рассматриваются на основе представлений и методов квантовой механики. Литовский язык, язык литовцев, распространён главным образом в Литовской. Несессер (франц. necessaire, буквально — необходимый), 1) дорожный футляр или небольшой чемодан с предметами туалета. Посошная рать, рекруты-крестьяне в России 16—17 вв. Синерво Эльви Ауликки Синерво (Sinervo) Эльви Ауликки (р 4.5.1912, Хельсинки), финская писательница, переводчица. Турнефор Жозеф Турнефоp (Tournefort) Жозеф (5.6.1656, Экс-ан-Прованс, — 28. Шевронное колесо, цилиндрическое зубчатое колесо с V-образными (угловыми) косыми зубьями. Асдрени Александр Сотир Дренова Асдрени (Asdreni) Александр Сотир Дренова (11. Владикавказ, до 1931 название г. Орджоникидзе, столицы Северо-Осетинской АССР; с 1944 по 1954 — Дзауджикау. Дибич-Забалканский Иван Иванович (Иоганн Карл Фридрих Антон) [2(13). Каротиноиды, жёлтые, оранжевые или красные пигменты (циклические или ациклические изопреноиды), синтезируемые бактериями, грибами и высшими растениями. Лех (Lech), река в Австрии и ФРГ, правый приток Дуная. Нафталинсульфокислоты, производные нафталина общей формулы C10H8-n (SO3H) n, где n = 1, 2, 3 или 4; кристаллические вещества, хорошо растворимые в воде и минеральных кислотах. Поллак Михай Поллак (Pollack) Михай (30.8.1773, Вена, — 5. Сердитое, посёлок городского типа в Донецкой области УССР. Тригонометрические функции, один из важнейших классов элементарных функций. Чон Бон Джун (1853—1895), руководитель крестьянского восстания в Корее. |
|