Шаровые функции
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ШАА |
| ШАБ |
| ШАВ |
| ШАГ |
| ШАД |
| ШАЖ |
| ШАИ |
| ШАЙ |
| ШАК |
| ШАЛ |
| ШАМ |
| ШАН |
| ШАО |
| ШАП |
| ШАР |
| ШАС |
| ШАТ |
| ШАУ |
| ШАФ |
| ШАХ |
| ШАЦ |
| ШАШ |
Шаровые функции, однородные функции un степени п от прямоугольных координат х, у, z, удовлетворяющие уравнению Лапласа:
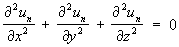
Существуют 2n + 1 линейно-независимых однородных многочленов от х, у, z целой положительной степени n, являющихся Шаровые функции: их линейная комбинация представляет общий вид такого многочлена степени n. Так, например,
uo= a, u1 = ax + by +cz;
u2 = a (x2 — z2) + b (y2 — z2) + cxy + dyz + ezx,
где a, b, с, d, e — произвольные постоянные, представляют общий вид однородных многочленов степеней 0, 1, 2, являющихся Шаровые функции Если вместо прямоугольных координат х, у, z ввести сферические координаты r, q, j, то Шаровые функции выражаются через сферические функции Yп (q,j) по формуле
un = rn Yn (q,j).
Каждой Шаровые функции un степени n соответствует Шаровые функции r¾2n¾1 степени — n—1.
Шаровые функции применяются при нахождении общего решения уравнения Лапласа и при решении задач математической физики для областей, ограниченных сферическими поверхностями.
Лит. см. при статье Сферические функции.
|
Так же Вы можете узнать о... Вашгерд (нем. Waschherd), промывочное устройство в виде наклонного стола для обогащения песков россыпей. Гаструла (позднелат. gastrula, от греч. gaster — желудок, чрево), одна из стадий зародышевого развития многоклеточных животных. Дальтониды и бертоллиды, термины, введённые Н. Жемчужная, река на юго-востоке Китая, рукав дельты р. Йотуни Мария Йотуни (Jotuni) Мария (9.4.1880, Куопио, — 30. Кодекс (системат. законодат. акт) Кодекс (лат. codex), единый систематизированный законодательный акт, в котором содержатся нормы права, регулирующие какую-либо определённую отрасль общественных отношений (например, уголовный К. Курбевуа (Courbevoie), город на С. Франции, северо-западный промышленный пригород Парижа, в департаменте О-де-Сен, на берегу р. Маква (макуа) язык, язык народности макуа в Мозамбике. Монтень Мишель де Монтень (Montaigne) Мишель де (28.2.1533, замок Монтень, близ Бордо, — 13. Оборачивающая призма, см. Оборачивающая система. Персей (царь Македонии) Персей (греч. Perseus) (около 213—166 до н. э. Противосудорожные средства, группа различных по химической природе лекарств, препаратов, обладающих способностью предупреждать или ослаблять судороги. |
|