Сходимость
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| СХА |
| СХЕ |
| СХИ |
| СХО |
| СХР |
| СХУ |
Сходимость, математическое понятие, означающее, что некоторая переменная величина имеет предел. В этом смысле говорят о Сходимость последовательности, Сходимость ряда, Сходимость бесконечного произведения, Сходимость непрерывной дроби, Сходимость интеграла и т. д. Понятие Сходимость возникает, например, когда при изучении того или иного математического объекта строится последовательность более простых в известном смысле объектов, приближающихся к данному, то есть имеющих его своим пределом (так, для вычисления длины окружности используется последовательность длин периметров правильных многоугольников, вписанных в окружность; для вычисления значений функций используются последовательности частичных сумм рядов, которыми представляются данные функции, и т. п.).
Сходимость последовательности {an}, n = 1, 2,..., означает существование у неё конечного предела  ; Сходимость ряда
; Сходимость ряда  — конечного предела (называемого суммой ряда) у последовательности его частичных сумм
— конечного предела (называемого суммой ряда) у последовательности его частичных сумм  ,
,  ; Сходимость бесконечного произведения b1 b2... bn — конечного предела, не равного нулю, у последовательности конечных произведений pn = b1b2... bn, n = 1, 2,...;Сходимость интеграла
; Сходимость бесконечного произведения b1 b2... bn — конечного предела, не равного нулю, у последовательности конечных произведений pn = b1b2... bn, n = 1, 2,...;Сходимость интеграла  от функции f (x), интегрируемой по любому конечному отрезку [а, b],— конечного предела у интегралов при b®+µ, называется несобственным интегралом
от функции f (x), интегрируемой по любому конечному отрезку [а, b],— конечного предела у интегралов при b®+µ, называется несобственным интегралом .
.
Свойство Сходимость тех или иных математических объектов играет существенную роль как в вопросах теории, так и в приложениях математики. Например, часто используется представление каких-либо величин или функций с помощью сходящихся рядов; так, для основания натуральных логарифмов е имеется разложение его в сходящийся ряд
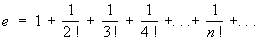
для функции sin х — в сходящийся при всех х ряд

Подобные ряды могут быть использованы для приближённого вычисления рассматриваемых величин и функций. Для этого достаточно взять сумму нескольких первых членов, при этом чем больше их взять, тем с большей точностью будет получено нужное значение. Для одних и тех же величин и функций имеются различные ряды, суммой которых они являются, например,
 ,
,
 .
.
При практических вычислениях в целях экономии числа операций (а следовательно, экономии времени и уменьшения накопления ошибок) целесообразно из имеющихся рядов выбрать ряд, который сходится «более быстро». Если даны два сходящихся ряда  и
и  , и
, и  ,
, 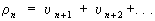 . — их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если
. — их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если
 .
.
Например, ряд

сходится быстрее ряда
 .
.
Используются и другие понятия «более быстро» сходящихся рядов. Существуют различные методы улучшения Сходимость рядов, то есть методы, позволяющие преобразовать данный ряд в «более быстро» сходящийся. Аналогично случаю рядов вводится понятие «более быстрой» Сходимость и для несобственных интегралов, для которых также имеются способы улучшения их Сходимость
Большую роль понятие Сходимость играет при решении всевозможных уравнений (алгебраических, дифференциальных, интегральных), в частности при нахождении их численных приближённых решений. Например, с помощью последовательных приближений метода можно получить последовательность функций, сходящихся к соответствующему решению данного обыкновенного дифференциального уравнения, и тем самым одновременно доказать существование при определённых условиях решения и дать метод, позволяющий вычислить это решение с нужной точностью. Как для обыкновенных дифференциальных уравнений, так и уравнений с частными производными существует хорошо разработанная теория различных сходящихся конечноразностных методов их численного решения (см. Сеток метод). Для практического нахождения приближённых решений уравнений широко используются ЭВМ.
Если изображать члены an последовательности {an} на числовой прямой, то Сходимость этой последовательности к а означает, что расстояние между точками anи а становится и остаётся сколь угодно малым с возрастанием n. В этой формулировке понятие Сходимость обобщается на последовательности точек плоскости, пространства и более общих объектов, для которых может быть определено понятие расстояния, обладающее обычными свойствами расстояния между точками пространства (например, на последовательности векторов, матриц, функций, геометрических фигур и т. д., см. Метрическое пространство). Если последовательность {an} сходится к а, то вне любой окрестности точки а лежит лишь конечное число членов последовательности. В этой формулировке понятие Сходимость допускает обобщение на совокупности величин ещё более общей природы, в которых тем или иным образом введено понятие окрестности (см. Топологическое пространство).
В математическом анализе используются различные виды Сходимость последовательности функций {fn (x)} к функции f (x) (на некотором множестве М). Если  для каждой точки X0 (из М), то говорят о Сходимость в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см. Мера множества), то говорят о Сходимость почти всюду]. Несмотря на свою естественность, понятие Сходимость в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из Сходимость функций fn (x) к f (x) в каждой точке не следует, вообще говоря, Сходимость интегралов от функций fn (x) к интегралу от f (x) и т. д.]. В связи с этим было введено понятие равномерной Сходимость, свободное от этих недостатков: последовательность {fn (x)} называется равномерно сходящейся к f (x) на множестве М, если
для каждой точки X0 (из М), то говорят о Сходимость в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см. Мера множества), то говорят о Сходимость почти всюду]. Несмотря на свою естественность, понятие Сходимость в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из Сходимость функций fn (x) к f (x) в каждой точке не следует, вообще говоря, Сходимость интегралов от функций fn (x) к интегралу от f (x) и т. д.]. В связи с этим было введено понятие равномерной Сходимость, свободное от этих недостатков: последовательность {fn (x)} называется равномерно сходящейся к f (x) на множестве М, если

Этот вид Сходимость соответствует определению расстояния между функциями f (x) и ( (х) по формуле
(х) по формуле

Д. Ф. Егоров доказал, что если последовательность измеримых функций сходится почти всюду на множестве М, то из М можно так удалить часть сколь угодно малой меры, чтобы на оставшейся части имела место равномерная Сходимость
В теории интегральных уравнений, ортогональных рядов и т. д. широко применяется понятие средней квадратической Сходимость: последовательность {fn (x)} сходится на отрезке [a, b] в среднем квадратическом к f (x), если
 .
.
Более общо, последовательность {fn (x)} сходится в среднем с показателем р к f (x), если
 .
.
Эта Сходимость соответствует заданию расстояния между функциями по формуле
 .
.
Из равномерной Сходимость на конечном отрезке вытекает Сходимость в среднем с любым показателем р. Последовательность частичных сумм разложения функции j(х) с интегрируемым квадратом по нормированной ортогональной системе функций может расходиться в каждой точке, но такая последовательность всегда сходится к j(х) в среднем квадратическом. Рассматриваются также другие виды Сходимость Например, Сходимость по мере: для любого e > 0 мера множества тех точек, для которых  , стремится к нулю с возрастанием n', слабая Сходимость:
, стремится к нулю с возрастанием n', слабая Сходимость:

для любой функции j(x) с интегрируемым квадратом (например, последовательность функций sinx, sin2x,..., sinnx,... слабо сходится к нулю на отрезке [—p, p], так как для любой функции j(х) с интегрируемым квадратом коэффициенты  ряда Фурье стремятся к нулю).
ряда Фурье стремятся к нулю).
Указанные выше и многие другие понятия Сходимость последовательности функций систематически изучаются в функциональном анализе, где рассматриваются различные линейные пространства с заданной нормой (расстоянием до нуля) — так называемые банаховы пространства. В таких пространствах можно ввести понятия Сходимость функционалов, операторов и т. д., определяя для них соответствующим образом норму. Наряду со Сходимость по норме (так называемой сильной Сходимость), в банаховых пространствах рассматривается слабая Сходимость, определяемая условием  для всех линейных функционалов; введённая выше слабая Сходимость функций соответствует рассмотрению нормы
для всех линейных функционалов; введённая выше слабая Сходимость функций соответствует рассмотрению нормы  . В современной математике рассматривается также Сходимость по частично упорядоченным множествам (см. Упорядоченные и частично упорядоченные множества). В теории вероятностей для последовательности случайных величин употребляются понятия Сходимость с вероятностью 1 и Сходимость по вероятности.
. В современной математике рассматривается также Сходимость по частично упорядоченным множествам (см. Упорядоченные и частично упорядоченные множества). В теории вероятностей для последовательности случайных величин употребляются понятия Сходимость с вероятностью 1 и Сходимость по вероятности.
Ещё математики древности (Евклид, Архимед) по существу употребляли бесконечные ряды для нахождения площадей и объёмов. Доказательством Сходимость рядов им служили вполне строгие рассуждения по схеме исчерпывания метода. Термин «Сходимость» в применении к рядам был введён в 1668 Дж. Грегори при исследовании некоторых способов вычисления площади круга и гиперболического сектора. Математики 17 в. обычно имели ясное представление о Сходимость употребляемых ими рядов, хотя и не проводили строгих с современной точки зрения доказательств С. В 18 в. широко распространилось употребление в анализе заведомо расходящихся рядов (в частности, их широко применял Л. Эйлер). Это, с одной стороны, привело впоследствии ко многим недоразумениям и ошибкам, устранённым лишь с развитием отчётливой теории Сходимость, а с другой — предвосхитило современную теорию суммирования расходящихся рядов. Строгие методы исследования Сходимость рядов были разработаны в 19 в. (О. Коши, Н. Абель, К. Вейерштрасс, Б. Больцано и др.). Понятие равномерной Сходимость было введено Дж. Стоксом. Дальнейшие расширения понятия Сходимость были связаны с развитием теории функций, функционального анализа и топологии.
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., т. 1—2, М., 1971—73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1—2, М., 1970; Никольский Сходимость М., Курс математического анализа, т. 1—2, М., 1973.
|
Так же Вы можете узнать о... Гарсиа Лорка Федерико Гарсиа Лорка (García Lorca) Федерико (5. Граувакка (от нем. grau — серый и Wacke — вид горной породы), горная порода осадочного происхождения, состоящая из мелких обломков (зёрен) осадочных и главным образом метаморфических и изверженных пород с примесью обломков основных вулканических горных пород и туфогенного материала; характерно значительное количество цементирующего материала. Диоскуриада, Диоскурия (греч. Dioskurias), античный город на побережье Чёрного моря (на месте современного г. Запятая плавающая, форма представления чисел в ЦВМ с переменным положением запятой, отделяющей целую часть числа от дробной. Истукан, статуя, которой поклоняются, как божеству; идол, кумир. Кестивен (Kesteven), часть графства Линкольншир в Великобритании. Коридзе Филимон Исаевич Коридзе (псевдоним — Кориджио) Филимон Исаевич (Ясеевич) (1829—1911), грузинский оперный певец (бас). Ламаркизм, первое целостное учение об эволюционном развитии живой природы, основные идеи которого были изложены Ж. Магнитная тонкая плёнка, полиили монокристаллический слой ферромагнитного металла, сплава или магнитного окисла (феррита и др. Мигание, защитный безусловный рефлекс (или образуемый на его основе условный рефлекс) в ответ на раздражение чувствительных ветвей тройничного нерва в роговице или в конъюнктиве глаза, коже век, ресницах, а также в ответ на световое раздражение. Нарком, см. в ст. Народный комиссариат. «Океанология», научный журнал Океанографической комиссии АН СССР. |
|