Положительно-определённая форма
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПОА |
| ПОБ |
| ПОВ |
| ПОГ |
| ПОД |
| ПОЕ |
| ПОЖ |
| ПОЗ |
| ПОИ |
| ПОЙ |
| ПОК |
| ПОЛ |
| ПОМ |
| ПОН |
| ПОО |
| ПОП |
| ПОР |
| ПОС |
| ПОТ |
| ПОУ |
| ПОХ |
| ПОЦ |
| ПОЧ |
| ПОШ |
| ПОЭ |
| ПОЯ |
Положительно-определённая форма, выражение вида 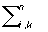 aikxixk,
aikxixk,
где aik= aki, принимающее неотрицательные значения при любых действительных значениях x1, х2,..., xn и обращающееся в нуль лишь при x1= х2=... = xn = 0. Т. о., Положительно-определённая форма есть квадратичная форма специального типа. Любая Положительно-определённая форма приводится с помощью линейного преобразования к виду 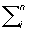 x2i
x2i
Для того чтобы 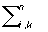 aikxixk
aikxixk
была Положительно-определённая форма необходимо и достаточно, чтобы D1 > 0, …, Dn > 0, где 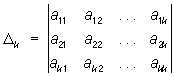
В любой аффинной системе координат расстояние точки от начала координат выражается Положительно-определённая форма от координат точки. Форма 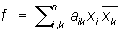 ,
,
(где 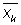 — число, комплексно сопряжённое с xk, см. Комплексные числа) такая, что aik=
— число, комплексно сопряжённое с xk, см. Комплексные числа) такая, что aik=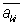 и f ³0 для всех значений x1, х2,..., xn и f = 0 лишь при x1 = х2=...= xn = 0, называется эрмитовой П.о. ф.
и f ³0 для всех значений x1, х2,..., xn и f = 0 лишь при x1 = х2=...= xn = 0, называется эрмитовой П.о. ф.
С понятием Положительно-определённая форма связаны также понятия: 1) положительно-определённой матрицы ||aik|| — такой матрицы, что 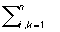 aikxixk
aikxixk
есть эрмитова Положительно-определённая форма;
2) положительно-определённого ядра — такой функции К (х, у) = 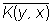 , что
, что 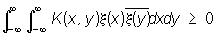
для любой функции x(х) с интегрируемым квадратом; 3) положительно-определённой функции — такой функции f (x), что ядро К (х, у) = f (x y) является положительно-определённым. Класс непрерывных положительно-определённых функций f (x) c f (0) = 1 совпадает с классом характеристических функций законов распределения случайных величин.
|
Так же Вы можете узнать о... ...фикация (от лат. facio – делаю) часть сложных слов, обозначающая делание, устройство (например, электрификация). Хеджази Сеид Мохаммед Багер (р. 1896), иранский писатель. Чагос (архипелаг) Чагос (Chagos), архипелаг в Индийском океане. Ширма Григорий Романович [р. 8(20).1. 1892, дер. Эндартериит облитерирующий (от греч. endon — внутри, артерии и облитерация), спонтанная гангрена, хроническое заболевание периферических кровеносных сосудов человека, с преимущественным поражением артерий стоп и голеней, уменьшением их просвета и нарушением кровоснабжения тканей. Автономность в системах связанного регулирования, независимость какой-либо одной из управляемых величин от изменений остальных управляемых величин (см. Андрей Боголюбский (около 1111 — 1174), князь владимиро-суздальский с 1157, сын Юрия Долгорукого, который и посадил А. Бабст Иван Кондратьевич (20.10.1823 — 6.7.1881), русский буржуазный историк и экономист. Бетьюн Нормен Бетьюн (Bethune) Нормен (4.3.1890 — 13.11.1939), канадский хирург, общественный деятель-антифашист, член Рабочей прогрессивной партии Канады. Булатович Александр Ксаверьевич [26.9(8.10). |
|