Определитель
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ОПА |
| ОПЕ |
| ОПЁ |
| ОПИ |
| ОПЛ |
| ОПО |
| ОПП |
| ОПР |
| ОПС |
| ОПТ |
| ОПУ |
| ОПЫ |
| ОПЬ |
Определитель, детерминант, особого рода математическое выражение, встречающееся в различных областях математики. Пусть дана матрица порядка n, т. е. квадратная таблица, составленная из п2 элементов (чисел, функций и т. п.): 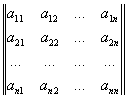 (1)
(1)
(каждый элемент матрицы снабжён двумя индексами: первый указывает номер строки, второй — номер столбца, на пересечении которых находится этот элемент). Определителем матрицы (1) называется многочлен, каждый член которого является произведением n элементов матрицы (1), причём из каждой строки и каждого столбца матрицы в произведение входит лишь один сомножитель, т. е. многочлен вида å±a1aa2b...ang. (2)
В этой формуле a, b, ..., g есть произвольная перестановка чисел 1, 2, ..., n. Перед членом берётся знак +, если перестановка a, b, ..., g чётная, и знак – , если эта перестановка нечётная. [Перестановку называют чётной, если в ней содержится чётное число нарушений порядка (или инверсий), т. е. случаев, когда большее число стоит впереди меньшего, и нечётной – в противоположном случае; так, например, перестановка 51243 – нечётная, т. к. в ней имеется 5 инверсий 51, 52, 54, 53, 43.] Суммирование производится по всем перестановкам a, b, ..., g чисел 1, 2, ..., n. Число различных перестановок n символов равно n! = 1·2·3·...·n; поэтому Определительсодержит n! членов, из которых 1/2n! берётся со знаком + и 1/2n! со знаком –. Число n называется порядком Определитель
Определитель, составленный из элементов матрицы (1), записывают в виде:  (3)
(3)
(или, сокращённо, в виде |aik|). Для Определитель 2-го и 3-го порядков имеем формулы: 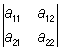 = a11a22 – a12a21,
= a11a22 – a12a21,
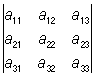 = a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.
= a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.
Определитель 2-го и 3-го порядков допускают простое геометрическое истолкование: 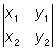 равен площади параллелограмма, построенного на векторах a1 = (x1, y1) и a2 = (х2.у2), а
равен площади параллелограмма, построенного на векторах a1 = (x1, y1) и a2 = (х2.у2), а 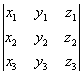 равен объёму параллелепипеда, построенного на векторах a1 = (x1, y1, z1), a2 = (x2, у2, z2) и а3 = (х3, y3, z3) (системы координат предполагаются прямоугольными).
равен объёму параллелепипеда, построенного на векторах a1 = (x1, y1, z1), a2 = (x2, у2, z2) и а3 = (х3, y3, z3) (системы координат предполагаются прямоугольными).
Теория Определитель возникла в связи с задачей решения систем алгебраических уравнений 1-й степени (линейные уравнения). В наиболее важном случае, когда число уравнений равно числу неизвестных, такая система может быть записана в виде: 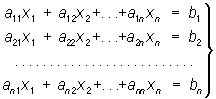 (4)
(4)
Эта система имеет одно определённое решение, если Определитель |aik|, составленный из коэффициентов при неизвестных, не равен нулю; тогда неизвестное xm(m = 1, 2, ..., n) равно дроби, у которой в знаменателе стоит Определитель|aik|, а в числителе — Определитель, получаемый из |aik| заменой элементов m-го столбца (т. е. коэффициентов при хт) числами b1, b2, ..., bn. Так, в случае системы двух уравнений с двумя неизвестными 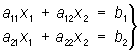
решение даётся формулами 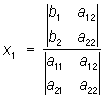 ;
; 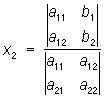 .
.
Если b1 = b2 = ..., = bn= 0, то систему (4) называется однородной системой линейных уравнений. Однородная система имеет отличные от нуля решения, только если |aik| = 0. Связь теории Определитель с теорией линейных уравнений позволила применить теорию Определитель к решению большого числа задач аналитической геометрии. Многие формулы аналитической геометрии удобно записывать при помощи Определитель; например, уравнение плоскости, проходящей через точки с координатами (x1, y1, z1), (x2, y2, z2), (х3, y3, z3), может быть записано в виде: 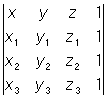 = 0.
= 0.
Определитель обладают рядом важных свойств, которые, в частности, облегчают их вычисление. Простейшие из этих свойств следующие:
1) O. не изменяется, если в нём строки и столбцы поменять местами:  =
= 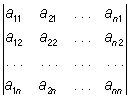 ;
;
2) Определитель меняет знак, если в нём поменять местами две строки (или два столбца); так, например: 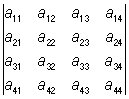 = –
= –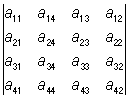 ;
;
3) Определитель равен нулю, если в нём элементы двух строк (или двух столбцов) соответственно пропорциональны; так, например: 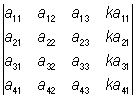 = 0;
= 0;
4) общий множитель всех элементов строки (или столбца) Определитель можно вынести за знак Определитель; так, например: 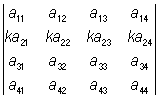 = k
= k 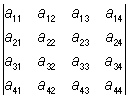 ;
;
5) если каждый элемент какого-нибудь столбца (строки) Определитель есть сумма двух слагаемых, то Определитель равен сумме двух Определитель, причём в одном из них соответствующий столбец (строка) состоит из первых слагаемых, а в другом — из вторых слагаемых, остальные же столбцы (строки) — те же, что и в данном Определитель; так, например: 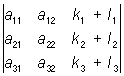 =
= 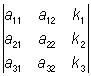 +
+ 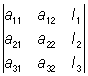 ;
;
6) Определитель не изменяется, если к элементам одной строки (столбца) прибавить элементы другой строки (другого столбца), умноженные на произвольный множитель; так, например:
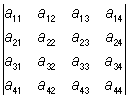 =
= 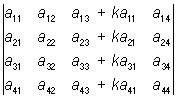 ;
;
7) Определитель может быть разложен по элементам какой-либо строки или какого-либо столбца. Разложение Определитель (3) по элементам i-й строки имеет следующий вид: 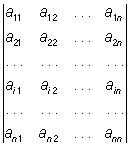 = ai1A i1 + ai2Ai2 + ...+ainAin.
= ai1A i1 + ai2Ai2 + ...+ainAin.
Коэффициент Aik, стоящий при элементе aik в этом разложении, называется алгебраическим дополнением элемента aik. Алгебраическое дополнение может быть вычислено по формуле: Aik= (–1)i+ kDik, где Dik— минор (подопределитель, субдетерминант), дополнительный к элементу aik, то есть Определитель порядка n-1, получающийся из данного Определитель посредством вычёркивания строки и столбца, на пересечении которых находится элемент aik. Например, разложение Определитель 3-го порядка по элементам второго столбца имеет следующий вид:
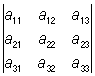 = –a12
= –a12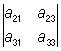 + a22
+ a22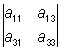 – a32
– a32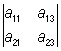 .
.
Посредством разложения по элементам строки или столбца вычисление Определитель n-го порядка приводится к вычислению n определителей (n 1)-го порядка. Так, вычисление Определитель 5-го порядка приводится к вычислению пяти Определитель 4-го порядка; вычисление каждого из этих Определитель 4-го порядка можно, в свою очередь, привести к вычислению четырёх Определитель 3-го порядка (формула для вычисления Определитель 3-го порядка приведена выше). Однако, за исключением простейших случаев, этот метод вычисления Определитель практически применим лишь для Определитель сравнительно небольших порядков. Для вычисления Определитель большого порядка разработаны различные, практически более удобные методы (для вычисления Определитель n-го порядка приходится выполнять примерно n3 арифметических операций).
Отметим ещё правило умножения двух Определитель n-го порядка: произведение двух Определитель n-го порядка может быть представлено в виде Определитель того же n-го порядка, в котором элемент, принадлежащий i-й строке и k-му столбцу, получается, если каждый элемент i-й строки первого множителя умножить на соответствующий элемент k-го столбца второго множителя и все эти произведения сложить; иными словами, произведение Определитель двух матриц равно Определитель произведения этих матриц.
В математическом анализе Определитель систематически используются после работ немецкого математика К. Якоби (2-я четверть 19 в.), исследовавшего Определитель, элементы которых являются не числами, а функциями одного или нескольких переменных. Из таких Определитель наибольший интерес представляет определитель Якоби (якобиан)  .
.
Определитель Якоби равен коэффициенту искажения объёмов при переходе от неременных х1, x2, ..., хп к переменным y1 = f1(x1, ..., xn), y2 = f2(x1, ..., xn), …………………. yn = fn(x1, ..., xn).
Тождественное равенство в некоторой области этого Определитель нулю является необходимым и достаточным условием зависимости функций f1(x1, ..., xn), f2(x1, ..., xn), ..., fn(x1, ..., xn).
Во 2-й половине 19 в. возникла теория Определитель бесконечного порядка. Бесконечными Определитель называются выражения вида: 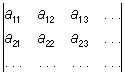 (5)
(5)
(односторонний бесконечный Определитель) и 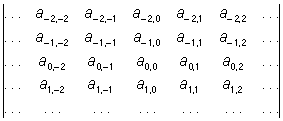
(двусторонний бесконечный Определитель). Бесконечный Определитель (5) есть предел, к которому стремится Определитель 
при бесконечном возрастании числа n. Если этот предел существует, то Определитель (5) называется сходящимся, в противном случае — расходящимся. Исследование двустороннего бесконечного Определитель иногда можно привести к исследованию некоторого одностороннего бесконечного Определитель
Теория Определитель конечного порядка создана в основном во 2-й половине 18 в. и 1-й половине 19 в. (работами швейцарского математика Г. Крамера, французских математиков А. Вандермонда, П. Лапласа, Определитель Коши, немецких математиков К. Гаусса и К. Якоби). Термин «Определитель» («детерминант») принадлежит К. Гауссу, современное обозначение — английскому математику А. Кэли.
Лит. см. при статьях Линейная алгебра,Матрица.
|
Так же Вы можете узнать о... Оцон-маньт, группа палеолитических местонахождений в Южно-Гобийском аймаке на Ю. Племя, тип этнической общности и социальной организации доклассового общества. Протодерма (от прото... и греч. derma — кожа), наружный слой клеток верхушечной меристемы побега и корня. Розенберг Альфред Розенберг (Rosenberg) Альфред (12.1.1893, Таллин, — 16. Сенгор Леопольд Седар Сенгор (Senghor) Леопольд Седар (р. 9.10.1906, Жоаль, Сенегал), государственный деятель Сенегала, философ, поэт. Спарманния (Sparmannia), род растений семейства липовых. Тареев Евгений Михайлович [р. 13(25).5.1895, Псков], советский терапевт, академик АМН СССР (1948), заслуженный деятель науки РСФСР (1948), Герой Социалистического Труда (1965). Туннель, см. Тоннель. Флора (мифологич.) Флора, в древнеримской мифологии богиня цветов, юности и весеннего цветения. Цементуемая сталь, конструкционная сталь с низким содержанием углерода (обычно 0,1—0,25%), предназначенная для изготовления деталей, подвергаемых цементации. Шокальского пролив, в архипелаге Северная Земля, между островами Большевик и Октябрьская Революция, соединяет моря Карское и Лаптевых. Язгулем, Мазардара, Обимазар, река в Горно-Бадахшанской АО Таджикской ССР, правый приток Пянджа. Амьен (Amiens), город на севере Франции, на реке Сомма. Балмашёв Степан Валерианович [3(15).4.1881, Пинега Архангельской губернии, — 3(16). Бонн (Bonn; лат. Bonna или Castra Bonnensia), столица ФРГ. Верчелли (Vercelli), город в Северной Италии, в области Пьемонт, на З. Галлер Лев Михайлович [17(29).11. 1883 — 12. |
|