Почти периодическая функция
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПОА |
| ПОБ |
| ПОВ |
| ПОГ |
| ПОД |
| ПОЕ |
| ПОЖ |
| ПОЗ |
| ПОИ |
| ПОЙ |
| ПОК |
| ПОЛ |
| ПОМ |
| ПОН |
| ПОО |
| ПОП |
| ПОР |
| ПОС |
| ПОТ |
| ПОУ |
| ПОХ |
| ПОЦ |
| ПОЧ |
| ПОШ |
| ПОЭ |
| ПОЯ |
Почти периодическая функция, функция, значения которой при добавлении к аргументу надлежащим образом выбранных постоянных чисел (почти периодов) приближённо повторяются. Более точно: непрерывная функция f (x), определённая для всех действительных значений х, называется почти периодической, если для каждого e > 0 можно указать такое l = l (e), что в каждом интервале оси х длины l найдётся хотя бы одно число t = t(e), для которого при любом х выполняется неравенство |f (x +t) — f (x)| < e. Числа t называются почти периодами функции f (x). Периодическая функции суть частные случаи Почти периодическая функция; простейшие примеры Почти периодическая функция, не являющихся периодическими, получаются в результате сложения периодических функций с несоизмеримыми периодами, например cosx + cos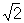 x.
x.
Некоторые наиболее важные свойства Почти периодическая функция:
1) Почти периодическая функция ограничена и равномерно непрерывна на всей оси х.
2) Сумма и произведение конечного числа Почти периодическая функция есть также Почти периодическая функция
3) Предел равномерно сходящейся последовательности Почти периодическая функция есть также Почти периодическая функция
4) Для каждой Почти периодическая функция существует среднее значение (на всей оси х):  .
.
5) Каждой Почти периодическая функция можно сопоставить ряд Фурье: 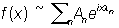 ,
,
причём l1, l2, …, ln, …, может быть любой последовательностью отличных друг от друга действительных чисел и 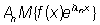 .
.
6) Равенство Парсеваля: для каждой Почти периодическая функция справедливо равенство: M {|f (x)|2} = 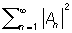 .
.
7) Теорема единственности: если f (x) есть непрерывная Почти периодическая функция и если для всех действительных l М {f (х) е-ilx} = 0,
то f (x) º 0. Иначе говоря, ряд Фурье однозначно определяет Почти периодическая функция
8) Теорема аппроксимации: для каждого e > 0 можно указать такой конечный тригонометрический полином 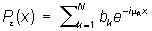
(mk — действительные числа), что для всех значений х выполняется неравенство: |f (x) — Pe(x)| < e; обратно, каждая функция f (x) с этим свойством является Почти периодическая функция
Первое построение непрерывных Почти периодическая функция было дано датским математиком Х. Бором (1923). Ещё ранее (1893) частный случай Почти периодическая функция — т. н. квазипериодические функции — изучил латвийский математик П. Боль. Новое построение теории Почти периодическая функция дал Н. Н. Боголюбов (1930). Обобщение теории Почти периодическая функция на разрывные функции впервые дано В. В. Степановым (1925), а потом Г. Вейлем и А. Безиковичем. Обобщение другого рода было дано советским математиком Б. М. Левитаном (1938).
Лит.: Бор Г., Почти периодические функции, пер. с нем., М. — Л., 1934; Левитан Б. М., Почти-периодические функции, М., 1953.
|
Так же Вы можете узнать о... Яно-Индигирская низменность, низменная равнина вдоль побережья морей Лаптевых и Восточно-Сибирского в Якутской АССР. Алунан Юрис Андреевич [1(13).5. 1832 — 6(18). Асдрени Александр Сотир Дренова Асдрени (Asdreni) Александр Сотир Дренова (11. Безмеин, город (до 1963 посёлок) в Туркменской ССР. Борзна, город, центр Борзнянского района Черниговской области УССР, на р. Ватт-час, внесистемная единица энергии или работы; равна работе, совершаемой за время 1 ч при мощности 1 вт. Волнолом, брекватер, гидротехническое сооружение для защиты от волнения (ветровых волн) акватории порта, рейдовых причалов, подходов к каналам и шлюзам, береговых участков моря, озера, водохранилища и т. Гели природные минеральные, аморфные минералы, образовавшиеся в водной среде и содержащие воду в переменных количествах. Городки, рюхи, чушки, русская народная игра, сущность которой состоит в том, чтобы бросками бит (палок) выбить из площадки («города» — отсюда название) поочерёдно определённое количество фигур, составленных из 5 городков — деревянных цилиндрических столбиков. Декантация (от франц. decanter — сцеживать, сливать), сливание жидкости с отстоявшегося осадка. Древнеисландский язык, язык, существовавший до середины 14 в. Затон (участок водн. пространства) Затон, защищенный от ледохода и течения участок водного пространства на судоходной реке, служащий для отстоя и ремонта судов. Интервьюирование, способ проведения социологических опросов как целенаправленной беседы интервьюера и опрашиваемого. Капуцин, род растений семейства настурциевых; то же, что настурция. Клавишные музыкальные инструменты, инструменты, звук в которых извлекается при помощи рычагов — клавиш, расположенных в определённом порядке и составляющих клавиатуру. Копулятивные органы, или совокупительные, органы животных, служащие у самцов для введения спермы в тело самки, а у самок — для принятия К. |
|