Функциональные уравнения
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ФУА |
| ФУВ |
| ФУГ |
| ФУД |
| ФУЖ |
| ФУЗ |
| ФУК |
| ФУЛ |
| ФУМ |
| ФУН |
| ФУР |
| ФУС |
| ФУТ |
| ФУЦ |
| ФУЧ |
| ФУШ |
| ФУЭ |
Функциональные уравнения, весьма общий класс уравнений, в которых искомой является некоторая функция. К Функциональные уравнения по существу относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях (см. Конечных разностей исчисление); следует, однако, отметить, что название «Функциональные уравнения» обычно не относят к уравнениям этих типов. Под Функциональные уравнения в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций [например, Функциональные уравнения (x) = f (—x) характеризует класс чётных функций, Функциональные уравнения f (x + 1) = f (x) — класс функций, имеющих период 1, и т.д.].
Одним из простейших Функциональные уравнения является уравнение f (x + у) = f (x) + f (y). Непрерывные решения этого Функциональные уравнения имеют вид f (x) = Cx. Однако в классе разрывных функций это Функциональные уравнения имеет и иные решения. С рассмотренным Функциональные уравнения связаны f (x + у) = f (x) f (y), f (xy) — f (x) + f (y), f (xy) = f (x) f (y),
непрерывные решения которых имеют соответственно вид eCx, Clnx, xa (x> 0). Т. о., эти Функциональные уравнения могут служить для определения показательной, логарифмической и степенной функций.
В теории аналитических функций Функциональные уравнения часто применяются для введения новых классов функций. Например, двоякопериодические функции характеризуются Функциональные уравнения f (z + а) = f (z) и f (z + b) = f (z), автоморфные функции — Функциональные уравнения f (saz) = f (z), где {sa} — некоторая группа дробно-линейных преобразований. Если функция известна в некоторой области, то знание для неё Функциональные уравнения позволяет расширить область определения этой функции. Например, Функциональные уравнения f (x + 1) = f (x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь Функциональные уравнения Г (z + 1) = zГ (z) и зная значения функции Г (z) (см. Гамма-функция) в полосе 0 £ Rez£ 1, можно продолжить её на всю плоскость z.
Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются Функциональные уравнения, которым должно удовлетворять решение данной задачи. Значение соответствующих Функциональные уравнения во многих случаях облегчает нахождение решений.
Решения Функциональные уравнения могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций. Для некоторых Функциональные уравнения общее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение Функциональные уравнения f (x) = f (ax) имеет вид j[w(x)], где j(x) — произвольная функция, а w(x) — частное решение этого Функциональные уравнения Для решения Функциональные уравнения их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций.
Другим методом решения Функциональные уравнения является метод итераций. Этот метод даёт, например, решение уравнения Абеля f[a(x)] = f (x) + 1 [где a(x) — заданная функция] и связанного с ним уравнения Шрёдера f[a(x)] = cf (x). А. Н. Коркин доказал, что если a(х) — аналитическая функция, то уравнение Абеля имеет аналитическое решение. Эти результаты, нашедшие применение в теории групп Ли (см. Непрерывные группы), привели в дальнейшем к созданию теории итераций аналитических функций. В некоторых случаях уравнение Абеля решается в конечном виде. Например, Функциональные уравнения f (xn) = f (x) + 1 имеет частное решение 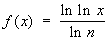 .
.
Лит.: Ацель Я., Некоторые общие методы в теории функциональных уравнений одной переменной. Новые применения функциональных уравнений, «Успехи математических наук», 1956, т. 11, в. 3, с. 3—68.
|
Так же Вы можете узнать о... Двинск, прежнее название г. Даугавпилса в Латвийской ССР. Ленгленд Уильям Ленгленд (Langland) Уильям (родился около 1330, Клэбери-Мортимер, Шропшир, — умер около 1400), английский поэт. Портулаковые (Portulacaceae), семейство двудольных растений. Унеча, город (с 1940), центр Унечского района Брянской обл. Бастия (Bastia), город и порт на северо-востоке острова Корсика (департамент Франции), на побережье Корсиканского пролива. Завриев Кириак Самсонович [р.16(28). 1.1891, Тбилиси], советский учёный в области строительной механики и сейсмостойкости сооружений, академик АН Грузинской ССР (1941), заслуженный деятель науки и техники Грузинской ССР. Медный век [иначе называется халколитом (от греческого chalkos — медь и lithos — камень) или энеолитом (от латинского aeneus — медный и греческого lithos — камень)], переходный период от неолита к бронзовому веку. Риччия (Riccia), род печёночных мхов семейства риччиевых. Хомутово, посёлок городского типа, центр Новодеревеньковского района Орловской области РСФСР. Валериана (Valeriana), маун, род многолетних травянистых растений семейства валериановых. Кальвиль белый зимний, сорт яблони французского происхождения. Натальская трава (Rhynchelytrum repens, или R. Система вала, система посадок для сопрягаемых гладких деталей машин, основной деталью (основанием) которой служит вал; характеризуется тем, что при данном номинальном размере сопрягаемых деталей предельные размеры вала остаются постоянными для всех посадок (см. Щугор, Щугырь, река в Коми АССР, правый приток Печоры. Гамбанг (gambang), индонезийский музыкальный ударный инструмент, деревянные или металлические пластинки, укрепленные на подставке в горизонтальном положении. Комо (город в Италии) Комо (Como), город в Северной Италии, в Ломбардии. Отопительно-вентиляционный агрегат, устройство для отопления и вентиляции преимущественно производственных помещений. Сырдарья (город в Узбекской ССР) Сырдарья, город (с 1971) областного подчинения, центр Сырдарьинского района Сырдарьинской области Узбекской ССР. |
|