Ортогональные многочлены
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ОРА |
| ОРБ |
| ОРВ |
| ОРГ |
| ОРД |
| ОРЕ |
| ОРЁ |
| ОРЖ |
| ОРИ |
| ОРК |
| ОРЛ |
| ОРМ |
| ОРН |
| ОРО |
| ОРП |
| ОРС |
| ОРТ |
| ОРУ |
| ОРФ |
| ОРХ |
| ОРШ |
| ОРЬ |
Ортогональные многочлены, специальные системы многочленов {рп (х)}; n = 0, 1, 2,..., ортогональных с весом r(х) на отрезке [а, b ] (см. Ортогональная система функций). Нормированная система Ортогональные многочлены обозначается через 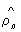 , а система Ортогональные многочлены, старшие коэффициенты которых равны 1,— через
, а система Ортогональные многочлены, старшие коэффициенты которых равны 1,— через 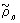 . В краевых задачах математической физики часто встречаются системы Ортогональные многочлены, для которых вес r(х) удовлетворяет дифференциальному уравнению (Пирсона)
. В краевых задачах математической физики часто встречаются системы Ортогональные многочлены, для которых вес r(х) удовлетворяет дифференциальному уравнению (Пирсона) 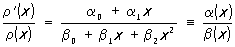
Многочлен рп (х) такой системы удовлетворяет дифференциальному уравнению 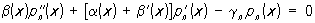
где gn=n [(a1 + (n + 1)b2].
Наиболее важные системы Ортогональные многочлены (классические) относятся к этому типу; они получаются (с точностью до постоянного множителя) при указанных ниже а, b и r(х).
1) Якоби многочлены {Рп (l,m)(х)} — при а = —1, b = 1 r(х) = (1—х)l (1 + x)m, l > —1, m > —1. Специальные частные случаи многочленов Якоби соответствуют следующим значениям l и m: l = m— ультрасферические многочлены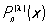 (их иногда называют многочленами Гегенбауэра); l = m = —1/2, т. е.
(их иногда называют многочленами Гегенбауэра); l = m = —1/2, т. е. 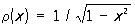 — Чебышева многочлены 1-го рода Tn (x); l = m = 1/2, т. е.
— Чебышева многочлены 1-го рода Tn (x); l = m = 1/2, т. е. 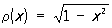 — Чебышева многочлены 2-го рода Un (x); l = m = 0, т. е. r(х)º1 — Лежандра многочленыРп (х).
— Чебышева многочлены 2-го рода Un (x); l = m = 0, т. е. r(х)º1 — Лежандра многочленыРп (х).
2) Лагерра многочленыLn (x) — при а = 0, b = + ¥ и r(х) = е—х (их наз. также многочленами Чебышева — Лагерра) и обобщённые многочлены Лагерра 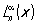 — при
— при 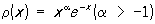 .
.
3) Эрмита многочленыНn (х) — при а = —¥, b = + ¥ и 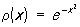 (их называют также многочленами Чебышева — Эрмита).
(их называют также многочленами Чебышева — Эрмита).
Ортогональные многочлены обладают многими общими свойствами. Нули многочленов рn (х) являются действительными и простыми и расположены внутри [а, b ]. Между двумя последовательными нулями многочлена рn (х) лежит один нуль многочлена pn+1(х). Многочлен рn (х) может быть представлен в виде т. н. формулы Родрига
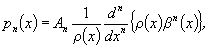
где An — постоянное, а b(х) см. формулу (*). Каждая система Ортогональные многочлены обладает свойствами замкнутости. Три последовательных Ортогональные многочлены 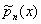 ,
, 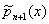 ,
,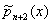 связаны рекуррентным соотношением:
связаны рекуррентным соотношением: 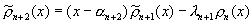 ,
,
где ап+2 и ln+2 следующим образом выражаются через коэффициенты этих многочленов: если 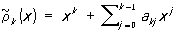 ,
,
то 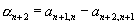 ;
; 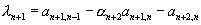
Общая теория Ортогональные многочлены построена П. Л. Чебышевым. Основным аппаратом изучения Ортогональные многочлены явилось для него разложение интеграла 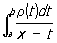 в непрерывную дробь с элементами вида х — an и числителями ln—1. Знаменатели jn (х)/рn (х) подходящих дробей этой непрерывной дроби образуют систему Ортогональные многочлены на отрезке [a, b ] относительно веса r(х).
в непрерывную дробь с элементами вида х — an и числителями ln—1. Знаменатели jn (х)/рn (х) подходящих дробей этой непрерывной дроби образуют систему Ортогональные многочлены на отрезке [a, b ] относительно веса r(х).
Приведённые выше классические системы Ортогональные многочлены выражаются через гипергеометрическую функцию.
Лит.: Сеге Г., Ортогональные многочлены, пер. с англ., М., 1962; см. также лит. при ст. Ортогональная система функций.
В. И. Битюцков.
|
Так же Вы можете узнать о... Булгуннях, местное (якут.) название мерзлотной формы рельефа — гидролакколита (см. Венгерская советская республика 1919 (ВСР), государство диктатуры пролетариата в Венгрии, существовавшее с 21 марта по 1 августа 1919. Военторг, система торговли, предназначенная для торгово-бытового обслуживания военнослужащих, членов их семей, рабочих и служащих Советской Армии и ВМФ. Гайярдия (Gaillardia), род травянистых многолетних или однолетних растений семейства сложноцветных. Гидасп (Hydaspes), древнегреческое наименование р. Гото Симпэй (14. 6. 1857, Мидзусава, — 13. 4. Даюйлин, горный хребет на юго-востоке Китая, в восточной части горной системы Наньлин, в провинции Гуандун и частично Цзянси. Динамометрический ключ, один из распространённых типов гаечных ключей. Евреи, общее этническое название (на русском языке) народностей, исторически восходящих к древним евреям. Захаров Семен Егорович [р. 10(23).1.1906, с. Ильи Святого гора (Saint Elias Mount), одна из самых высоких вершин в массиве гор Святого Ильи, на границе Канады и Аляски. |
|