Потенциалы электромагнитного поля
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПОА |
| ПОБ |
| ПОВ |
| ПОГ |
| ПОД |
| ПОЕ |
| ПОЖ |
| ПОЗ |
| ПОИ |
| ПОЙ |
| ПОК |
| ПОЛ |
| ПОМ |
| ПОН |
| ПОО |
| ПОП |
| ПОР |
| ПОС |
| ПОТ |
| ПОУ |
| ПОХ |
| ПОЦ |
| ПОЧ |
| ПОШ |
| ПОЭ |
| ПОЯ |
Потенциалы электромагнитного поля, величины, характеризующие электромагнитное поле. В электростатике векторное электрическое поле можно характеризовать одной скалярной функцией — потенциалом электростатическим. В общем случае для описания произвольного электромагнитного поля вместо двух векторов — магнитной индукции В и напряжённости электрического поля Е можно ввести две др. величины: векторный потенциал А (х, у, z, t) и скалярный потенциал j(x, у, z, t) (где х, у, z — координаты, t — время), при этом В и Е однозначно выражаются через А и j В = rot А, E = -gradj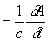 , (1)
, (1)
где с — скорость света в вакууме.
Уравнения для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения, и поэтому введение Потенциалы электромагнитного поля упрощает задачу нахождения переменных электромагнитных полей. Существенное упрощение уравнений для Потенциалы электромагнитного поля возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и j выбрать новые потенциалы А' = А + gradc, 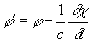 , (2)
, (2)
где c — произвольная функция координат и времени, то векторы В и Е, определяемые уравнениями (1), не изменятся. Инвариантность электромагнитного поля по отношению к преобразованиям потенциалов (2) носит название калибровочной или градиентной инвариантности. Калибровочная инвариантность позволяет наложить на Потенциалы электромагнитного поля дополнительное условие. Обычно таким дополнительным условием является условие Лоренца: divA + 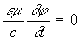 , (3)
, (3)
где e и m— диэлектрическая и магнитная проницаемости среды. При использовании условия (3) уравнения для Потенциалы электромагнитного поля в однородной среде (e = const, m = const), получаемые из уравнений Максвелла, приобретают одинаковую форму: 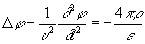 , (4)
, (4) 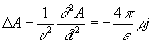 ;
;
здесь D—Лапласа оператор, r и j — плотности заряда и тока, a u = 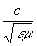 — скорость распространения электромагнитного поля в среде. Если r = 0 и j = 0, то Потенциалы электромагнитного поля удовлетворяют волновым уравнениям.
— скорость распространения электромагнитного поля в среде. Если r = 0 и j = 0, то Потенциалы электромагнитного поля удовлетворяют волновым уравнениям.
Уравнения (4) позволяют определить потенциалы А и j по известному распределению зарядов и токов, а следовательно, с помощью формул (1) — характеристики электромагнитного поля В и Е. Частные решения уравнений (4), удовлетворяющие причинности принципу, называют запаздывающими потенциалами. Запаздывающие потенциалы в точке с координатами х, у, z в момент времени t определяются плотностями заряда и тока в точке с координатами х’, у’, z' в предшествующий момент времени t = t — R/u, где 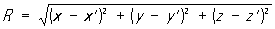
— расстояние от источника поля до точки наблюдения.
Если заряды и токи распределены в конечной области пространства G, то запаздывающие потенциалы определяются суммированием (интегрированием) элементарных потенциалов от зарядов и токов, сосредоточенных в бесконечно малых объёмах dx'dy'dz’, с учётом времени запаздывания: j (х, у, z, t) = 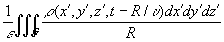 , A (х, у, z, t) =
, A (х, у, z, t) = 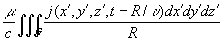 ,
,
Через Потенциалы электромагнитного поля выражается функция Гамильтона Н заряженной частицы, движущейся в электромагнитном поле: 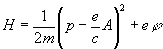 , (6)
, (6)
где p — импульс частицы, e и m — ее заряд и масса. Соответственно через Потенциалы электромагнитного поля выражается оператор Гамильтона (гамильтониан) в квантовой механике.
Лит. см. при ст. Максвелла уравнения.
Г. Я. Мякишев.
|
Так же Вы можете узнать о... Утена, город, центр Утенского района Литовской ССР. Фосфатиды, то же, что фосфолипиды. Ходжкин Алан Ллойд Ходжкин (Hodgkin) Алан Ллойд (р. 5.2.1914, Банбери, Оксфордшир), английский физиолог, член Лондонского королевского общества (1948, в 1970—75 — президент). Чекан, инструмент для чеканки, имеющий форму зубила, рабочая кромка которого затуплена и закруглена. Широковский, посёлок городского типа в Пермской области РСФСР, подчинён Губахинскому горсовету. Элефанта, Гхарапури, остров в Аравийском море, в 8 км от Бомбея. Ярославский университет, 1) высшее учебное заведение, основанное в г. Александрийская библиотека, наиболее известная в древности библиотека, основанная в Александрии при Александрийском мусейоне в начале 3 в. Аптекарский приказ, высшее государственное медицинское административное учреждение в России 16—17 вв. Байдара, русское название лодки приморских чукчей, коряков и эскимосов, состоящей из деревянного каркаса, обтянутого шкурой моржа (у эвенов Охотского побережья были также Б. Берисо (Berisso), город на В. Аргентины, в провинции Буэнос-Айрес. Брайант Луиза Брайант (Bryant) Луиза (1890 — 1936), американская писательница и журналистка. Варьете (франц. variete, от лат. varietas — разнообразие, пестрота), вид театра, в представлениях которого сочетаются различные жанры театрального, музыкального, эстрадного и циркового искусства. Внутренние воды (в международном праве), внутренние водные пути (реки, каналы, озёра, водохранилища, находящиеся на территории данного государства) и моря, ограниченные со всех сторон сушей, составляющей территорию только одного государства (например, Аральское море в СССР). Газотурбинный автомобиль, автомобиль, оборудованный газотурбинным двигателем. |
|