Математическая физика
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| МАА |
| МАБ |
| МАВ |
| МАГ |
| МАД |
| МАЕ |
| МАЁ |
| МАЖ |
| МАЗ |
| МАИ |
| МАЙ |
| МАК |
| МАЛ |
| МАМ |
| МАН |
| МАО |
| МАП |
| МАР |
| МАС |
| МАТ |
| МАУ |
| МАФ |
| МАХ |
| МАЦ |
| МАЧ |
| МАШ |
| МАЭ |
| МАЮ |
| МАЯ |
Математическая физика, теория математических моделей физических явлений; занимает особое положение и в математике, и в физике, находясь на стыке этих наук.
Математическая физика тесно связана с физикой в той части, которая касается построения математической модели, и в то же время — раздел математики, поскольку методы исследования моделей являются математическими. В понятие методов Математическая физика включаются те математические методы, которые применяются для построения и изучения математических моделей, описывающих большие классы физических явлений.
Методы Математическая физика как теории математических моделей физики начали интенсивно разрабатываться в трудах И. Ньютона по созданию основ классической механики, всемирного тяготения, теории света. Дальнейшее развитие методов Математическая физика и их успешное применение к изучению математических моделей огромного круга различных физических явлений связаны с именами Ж. Лагранжа, Л. Эйлера, П. Лапласа, Ж. Фурье, К. Гаусса, Б. Римана, М. В. Остроградского и многих других учёных. Большой вклад в развитие методов Математическая физика внесли А. М. Ляпунов и В. А. Стеклов. Начиная со 2-й половины 19 века методы Математическая физика успешно применялись для изучения математических моделей физических явлений, связанных с различными физическими полями и волновыми функциями в электродинамике, акустике, теории упругости, гидрои аэродинамике и ряде других направлений исследования физических явлений в сплошных средах. Математические модели этого класса явлений наиболее часто описываются при помощи дифференциальных уравнений с частными производными, получивших название уравнений математической физики. Помимо дифференциальных уравнений Математическая физика, при описании математических моделей физики применение находят интегральные уравнения и интегро-дифференциальные уравнения, вариационные и теоретико-вероятностные методы, теория потенциала, методы теории функций комплексного переменного и ряд других разделов математики. В связи с бурным развитием вычислительной математики особое значение для исследования математических моделей физики приобретают прямые численные методы, использующие ЭВМ, и в первую очередь конечно-разностные методы решения краевых задач. Теоретические исследования в области квантовой электродинамики, аксиоматической теории поля и ряде других направлений современной физики привели к созданию нового класса математических моделей, составивших важную отрасль Математическая физика (например, теория обобщённых функций, теория операторов с непрерывным спектром).
Постановка задач Математическая физика заключается в построении математических моделей, описывающих основные закономерности изучаемого класса физических явлений. Такая постановка состоит в выводе уравнений (дифференциальных, интегральных, интегро-дифференциальных или алгебраических), которым удовлетворяют величины, характеризующие физический процесс. При этом исходят из основных физических законов, учитывающих только наиболее существенные черты явления, отвлекаясь от ряда его второстепенных характеристик. Такими законами являются обычно законы сохранения, например, количества движения, энергии, числа частиц и т. д. Это приводит к тому, что для описания процессов различной физической природы, но имеющих общие характерные черты, оказываются применимыми одни и те же математические модели. Например, математические задачи для простейшего уравнения гиперболического типа
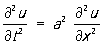 ,
,
полученного первоначально (Ж. Д’Аламбер, 1747) для описания свободных колебаний однородной струны, оказываются применимыми и для описания широкого круга волновых процессов акустики, гидродинамики, электродинамики и других областей физики. Аналогично, уравнение
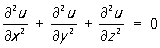 ,
,
краевые задачи для которого первоначально изучались П. Лапласом (конец 18 века) в связи с построением теории тяготения (см. Лапласа уравнение), в дальнейшем нашло применение при решении многих проблем электростатики, теории упругости, задач установившегося движения идеальной жидкости и т. д. Каждой математической модели физики соответствует целый класс физических процессов.
Для Математическая физика характерно также то, что многие общие методы, используемые для решения задач Математическая физика, развились из частных способов решения конкретных физических задач и в своём первоначальном виде не имели строгого математического обоснования и достаточной завершённости. Это относится к таким известным методам решения задач Математическая физика, как Ритца и Галёркина методы, к методам теории возмущении, преобразований Фурье и многим другим, включая метод разделения переменных. Эффективное применение всех этих методов для решения конкретных задач является одной из причин для их строгого математического обоснования и обобщения, приводящего в ряде случаев к возникновению новых математических направлений.
Воздействие Математическая физика на различные разделы математики проявляется и в том, что развитие Математическая физика, отражающее требования естественных наук и запросы практики, влечёт за собой переориентацию направленности исследований в некоторых уже сложившихся разделах математики. Постановка задач Математическая физика, связанная с разработкой математических моделей реальных физических явлений, привела к изменению основной проблематики теории дифференциальных уравнений с частными производными. Возникла теория краевых задач, позволившая впоследствии связать дифференциальные уравнения с частными производными с интегральными уравнениями и вариационными методами.
Изучение математических моделей физики математическими методами не только позволяет получить количественные характеристики физических явлений и рассчитать с заданной степенью точности ход реальных процессов, но и даёт возможность глубокого проникновения в самую суть физических явлений, выявления скрытых закономерностей, предсказания новых эффектов. Стремление к более детальному изучению физических явлений приводит к всё большему усложнению описывающих эти явления математических моделей, что, в свою очередь, делает невозможным применение аналитических методов исследования этих моделей. Это объясняется, в частности, тем, что математические модели реальных физических процессов являются, как правило, нелинейными, то есть описываются нелинейными уравнениями Математическая физика Для детального исследования таких моделей успешно применяются прямые численные методы с использованием ЭВМ. Для типичных задач Математическая физика применение численных методов сводится к замене уравнениями Математическая физика для функций непрерывного аргумента алгебраическими уравнениями для сеточных функций, заданных на дискретном множестве точек (на сетке). Иными словами, вместо непрерывной модели среды вводится её дискретный аналог. Применение численных методов в ряде случаев позволяет заменить сложный, трудоёмкий и дорогостоящий физический эксперимент значительно более экономичным математическим (численным) экспериментом. Достаточно полно проведённый математический численный эксперимент является основой для выбора оптимальных условий реального физического эксперимента, выбора параметров сложных физических установок, определения условий проявления новых физических эффектов и т. д. Таким образом численные методы необычайно расширяют область эффективного использования математических моделей физических явлений.
Математическая модель физического явления, как всякая модель, не может передать всех черт явления. Установить адекватность принятой модели исследуемому явлению можно только при помощи критерия практики, сопоставляя результаты теоретических исследований принятой модели с данными экспериментов.
Во многих случаях об адекватности принятой модели можно судить на основании решения обратных задач Математическая физика, когда о свойствах изучаемых явлений природы, недоступных для непосредственного наблюдения, делаются заключения по результатам их косвенных физических проявлений.
Для Математическая физика характерно стремление строить такие математические модели, которые не только дают описание и объяснение уже установленных физических закономерностей изучаемого круга явлений, но и позволяют предсказать ещё не открытые закономерности. Классическим примером такой модели является теория всемирного тяготения Ньютона, позволившая не только объяснить движение известных к моменту её создания тел Солнечной системы, но и предсказывать существование новых планет. С другой стороны, появляющиеся новые экспериментальные данные не всегда могут быть объяснены в рамках принятой модели. Для их объяснения требуется усложнение модели.
Лит.: Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972; Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; Соболев С. А., Уравнения математической физики, М., 1966; Курант Р., Уравнения с частными производными, перевод с английского, М., 1964; Морс Ф. М., Фешбах Г., Методы теоретической физики, перевод с английского, т. 1—2, М., 1958.
А. Н. Тихонов, А. А. Самарский, А. Г. Свешников.
|
Так же Вы можете узнать о... Обершпре (Kombinat VEB Kabelwerk Oberspree), кабельный комбинат в ГДР. Плеснеск, древнерусский город в верховьях р. Репарация в генетике, особая функция клеток, заключающаяся в способности исправлять химические повреждения и разрывы в молекулах дезоксирибонуклеиновой кислоты (ДНК), возникающие вследствие воздействия различных физических и химических агентов, а также при нормальном биосинтезе ДНК в процессе жизнедеятельности клеток. |
|