Топология 3. Алгебраическая топология
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ТОА |
| ТОБ |
| ТОВ |
| ТОГ |
| ТОД |
| ТОЁ |
| ТОЖ |
| ТОЗ |
| ТОИ |
| ТОЙ |
| ТОК |
| ТОЛ |
| ТОМ |
| ТОН |
| ТОО |
| ТОП |
| ТОР |
| ТОС |
| ТОТ |
| ТОУ |
| ТОФ |
| ТОХ |
| ТОЦ |
| ТОЧ |
| ТОШ |
| ТОЩ |
| ТОЯ |
3. Алгебраическая топология
Пусть каждому топологическому пространству Х (из некоторого класса) поставлен в соответствие некоторый алгебраический объект h(X) (группа, кольцо и т.п.), а каждому непрерывному отображению f : X®Y — некоторый гомоморфизм h(f) : h(X)®h(Y) (или h(f) : h(Y)®h(X), являющийся тождественным гомоморфизмом, когда f представляет собой тождественное отображение. Если h(f1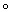 f2)= h(f1)
f2)= h(f1) 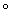 h(f2) (или, соответственно, h(f1
h(f2) (или, соответственно, h(f1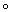 f2)= h(f2)
f2)= h(f2)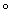 h(f1), то говорят, что h представляет собой функтор (соответственно кофунктор). Большинство задач алгебраической Топология так или иначе связано со следующей задачей распространения: для данного непрерывного отображения f : A ® Y подпространства AÌ Х в некоторое топологическое пространство Y найти непрерывное отображение g : X ® Y, совпадающее на A с f, то есть такое, что f=g×i, где i:А ®Х— отображение вложения (i(a) = а для любой точки а ÎA). Если такое непрерывное отображение g существует, то для любого функтора (кофунктора) h существует такой гомоморфизм (j: h(X)®h(Y) (гомоморфизм j: h(Y)®h(X)), что h(f) =j
h(f1), то говорят, что h представляет собой функтор (соответственно кофунктор). Большинство задач алгебраической Топология так или иначе связано со следующей задачей распространения: для данного непрерывного отображения f : A ® Y подпространства AÌ Х в некоторое топологическое пространство Y найти непрерывное отображение g : X ® Y, совпадающее на A с f, то есть такое, что f=g×i, где i:А ®Х— отображение вложения (i(a) = а для любой точки а ÎA). Если такое непрерывное отображение g существует, то для любого функтора (кофунктора) h существует такой гомоморфизм (j: h(X)®h(Y) (гомоморфизм j: h(Y)®h(X)), что h(f) =j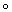 h(i) (соответственно h(f) =h(i)
h(i) (соответственно h(f) =h(i)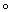 j); им будет гомоморфизм j= h(g). Следовательно, несуществование гомоморфизма j (хотя бы для одного функтора h) влечёт несуществование отображения g. К этому простому принципу могут быть фактически сведены почти все методы алгебраических Топология Например, существует функтор h, значение которого на шаре E n является тривиальной, а на ограничивающей шар сфере S n—1 — нетривиальной группой. Уже отсюда следует отсутствие так называемой ретракции — непрерывного отображения р : E n® S n—1, неподвижного на S n—1, то есть такого, что композиция р×i, где i : S n‑1 ® E n — отображение вложения, представляет собой тождественное отображение (если р существует, то тождественное отображение группы h(S n—1) будет композицией отображений h(i) : h(S n—1)®h(E n) и h(p) : h(E n)®h(S n—1), что при тривиальной группе h(E n) невозможно). Однако этот, по существу, элементарно-геометрический и (при n= 2) наглядно очевидный факт (физически означающий возможность натянуть на круглый обруч барабан) до сих пор не удалось доказать без привлечения алгебраико-топологических методов. Его непосредственным следствием является утверждение, что любое непрерывное отображение f : E n® E n имеет хотя бы одну неподвижную точку, то есть уравнение f(x) = х имеет в E n хотя бы одно решение (если f(x)¹x для всех хÎE n, то, приняв за р(х) точку из S n—1, коллинеарную точкам f(x) и х и такую, что отрезок с концами f(x) и р(х) содержит х, получим ретракцию р : E n®S n—1). Эта теорема о неподвижной точке была одной из первых теорем алгебраической Топология, а затем явилась источником целой серии разнообразных теорем существования решений уравнений.
j); им будет гомоморфизм j= h(g). Следовательно, несуществование гомоморфизма j (хотя бы для одного функтора h) влечёт несуществование отображения g. К этому простому принципу могут быть фактически сведены почти все методы алгебраических Топология Например, существует функтор h, значение которого на шаре E n является тривиальной, а на ограничивающей шар сфере S n—1 — нетривиальной группой. Уже отсюда следует отсутствие так называемой ретракции — непрерывного отображения р : E n® S n—1, неподвижного на S n—1, то есть такого, что композиция р×i, где i : S n‑1 ® E n — отображение вложения, представляет собой тождественное отображение (если р существует, то тождественное отображение группы h(S n—1) будет композицией отображений h(i) : h(S n—1)®h(E n) и h(p) : h(E n)®h(S n—1), что при тривиальной группе h(E n) невозможно). Однако этот, по существу, элементарно-геометрический и (при n= 2) наглядно очевидный факт (физически означающий возможность натянуть на круглый обруч барабан) до сих пор не удалось доказать без привлечения алгебраико-топологических методов. Его непосредственным следствием является утверждение, что любое непрерывное отображение f : E n® E n имеет хотя бы одну неподвижную точку, то есть уравнение f(x) = х имеет в E n хотя бы одно решение (если f(x)¹x для всех хÎE n, то, приняв за р(х) точку из S n—1, коллинеарную точкам f(x) и х и такую, что отрезок с концами f(x) и р(х) содержит х, получим ретракцию р : E n®S n—1). Эта теорема о неподвижной точке была одной из первых теорем алгебраической Топология, а затем явилась источником целой серии разнообразных теорем существования решений уравнений.
Вообще говоря, установление несуществования гомоморфизма (j тем легче, чем сложнее алгебраическая структура объектов h(X). Поэтому в алгебраических Топология рассматриваются алгебраические объекты чрезвычайно сложной природы, и требования алгебраической топологии существенно стимулировали развитие абстрактной алгебры.
Топологическое пространство Х называется клеточным пространством, а также клеточным разбиением (или CW-комплексом), если в нём указана возрастающая последовательность подпространств X 0̼ Ì X n—1Ì X n̼ (называется остовами клеточного пространства X), объединением которых является всё X, причём выполнены следующие условия: 1) множество UÌX тогда и только тогда открыто в X, когда для любого n множество U ÇX n открыто в X n; 2) X n получается из X n—1 приклеиванием некоторого семейства n-мepных шаров по их граничным (n—1)-мepным сферам (посредством произвольного непрерывного отображения этих сфер в X n—1); 3) X0 состоит из изолированных точек. Таким образом, структура клеточного пространства состоит, грубо говоря, в том, что оно представлено в виде объединения множеств, гомеоморфных открытым шарам (эти множества называются клетками). В алгебраических Топология изучаются почти исключительно клеточные пространства, поскольку специфика задач алгебраических Топология для них уже полностью проявляется. Более того, фактически для алгебраических Топология интересны некоторые особо простые клеточные пространства (типа полиэдров, см. ниже), но сужение класса клеточных пространств, как правило, существенно осложняет исследование (поскольку многие полезные операции над клеточными пространствами выводят из класса полиэдров).
Два непрерывных отображения f, g : X ® Y называются гомотопными, если они могут быть непрерывно продеформированы друг в друга, то есть если существует такое семейство непрерывных отображений ft : X ® Y, непрерывно зависящих от параметра t Î [0, 1], что f0= f и f1 = g (непрерывная зависимость от t означает, что формула F(x, t) = ft(x), хÎX, tÎ [0, 1] определяет непрерывное отображение F : Х´ [0, 1] ®Y; это отображение, а также семейство {ft } называют гомотопией, связывающей f с g). Совокупность всех непрерывных отображений X®Y распадается на гомотопические классы гомотопных между собой отображений. Множество гомотопических классов непрерывных отображений из Х в Y обозначается символом [X, Y]. Изучение свойств отношения гомотопности и, в частности, множеств [X, Y] составляет предмет так называемой гомотопической топологии (или теории гомотопий). Для большинства интересных топологических пространств множества [X, Y] конечны или счётны и могут быть в явном виде эффективно вычислены. Топологические пространства Х и Y называются гомотопически эквивалентными, или имеющими один и тот же гомотопический тип, если существуют такие непрерывные отображения f : Х®Y и g : Y® Х, что непрерывные отображения g×f : Х®Х и f×g : Y ® Y гомотопны соответствующим тождественным отображениям. В гомотопической Топология такие пространства следует рассматривать как одинаковые (все их «гомотопические инварианты» совпадают).
Оказывается, что во многих случаях (в частности, для клеточных пространств) разрешимость задачи распространения зависит только от гомотопического класса непрерывного отображения f : A®Y; точнее, если для f распространение g : Х®Y существует, то для любой гомотопии ft : A ® Y(с f0 = f) существует распространение gt : Х®Y такое, что g0 = g. Поэтому вместо f можно рассматривать его гомотопический класс [f] и в соответствии с этим изучать лишь гомотопически инвариантные функторы (кофункторы) h, то есть такие, что h(f0) = h(f1), если отображения f0 и f1 гомотопны. Это приводит к настолько тесному переплетению алгебраической и гомотопической Топология, что их можно рассматривать как единую дисциплину.
Для любого топологического пространства Y формулы h(X) = [X, Y] и h(f)= [j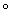 f], где f : X1®X2 и j : X2®Y, определяют некоторый гомотопически инвариантный кофунктор h, о котором говорят, что он представлен топологическим пространством Y. Это — стандартный (и по существу единственный) приём построения гомотопических инвариантных кофункторов. Чтобы множество h(X) оказалось, скажем, группой, нужно У выбрать соответствующим образом, например потребовать, чтобы оно было топологической группой (вообще говоря, это не совсем так: необходимо выбрать в Х некоторую точку x0 и рассматривать лишь непрерывные отображения и гомотопии, переводящие x0 в единицу группы; это техническое усложнение будет, однако, в дальнейшем игнорироваться). Более того, достаточно, чтобы Y было топологической группой «в гомотопическом смысле», то есть чтобы аксиомы ассоциативности и существования обратного элемента (утверждающие фактически совпадение некоторых отображений) выполнялись бы только «с точностью до гомотопии». Такие топологические пространства называются Н-пространствами. Таким образом, каждое Н-пространство Y задаёт гомотопически инвариантный кофунктор h(X) = [X, Y], значениями которого являются группы.
f], где f : X1®X2 и j : X2®Y, определяют некоторый гомотопически инвариантный кофунктор h, о котором говорят, что он представлен топологическим пространством Y. Это — стандартный (и по существу единственный) приём построения гомотопических инвариантных кофункторов. Чтобы множество h(X) оказалось, скажем, группой, нужно У выбрать соответствующим образом, например потребовать, чтобы оно было топологической группой (вообще говоря, это не совсем так: необходимо выбрать в Х некоторую точку x0 и рассматривать лишь непрерывные отображения и гомотопии, переводящие x0 в единицу группы; это техническое усложнение будет, однако, в дальнейшем игнорироваться). Более того, достаточно, чтобы Y было топологической группой «в гомотопическом смысле», то есть чтобы аксиомы ассоциативности и существования обратного элемента (утверждающие фактически совпадение некоторых отображений) выполнялись бы только «с точностью до гомотопии». Такие топологические пространства называются Н-пространствами. Таким образом, каждое Н-пространство Y задаёт гомотопически инвариантный кофунктор h(X) = [X, Y], значениями которого являются группы.
Аналогичным («двойственным») образом, каждое топологическое пространство Y задаёт по формулам h(X)= [Y, X], h(f) = [f 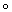 j], где f : X1®X2 и j : Y®X1, некоторый функтор h. Чтобы h(X) было группой, нужно, чтобы Y обладало определённой алгебраической структурой, в некотором точно определённом смысле двойственной структуре Н-пространства. Топологические пространства, наделённые этой структурой, называются ко-Н-пространствами. Примером ко-Н-пространства является n-мepная сфера S n (при n³1). Таким образом, для любого топологического пространства Х формула pnX= [S n, X] определяет некоторую группу pnX, n³1, которая называется n-й гомотопической группой пространства X. При n = 1 она совпадает с фундаментальной группой. При n > 1 группа pnX коммутативна. Если p1X = {1}, то Х называется односвязным.
j], где f : X1®X2 и j : Y®X1, некоторый функтор h. Чтобы h(X) было группой, нужно, чтобы Y обладало определённой алгебраической структурой, в некотором точно определённом смысле двойственной структуре Н-пространства. Топологические пространства, наделённые этой структурой, называются ко-Н-пространствами. Примером ко-Н-пространства является n-мepная сфера S n (при n³1). Таким образом, для любого топологического пространства Х формула pnX= [S n, X] определяет некоторую группу pnX, n³1, которая называется n-й гомотопической группой пространства X. При n = 1 она совпадает с фундаментальной группой. При n > 1 группа pnX коммутативна. Если p1X = {1}, то Х называется односвязным.
Клеточное пространство Х называется пространством K(G, n), если pi(X)= 0 при i¹n и pnX = G; такое клеточное пространство существует для любого n³ 1 и любой группы G (коммутативной при n > 1) и с точностью до гомотопической эквивалентности определено однозначно. При n > 1 (а также при n = 1, если группа G коммутативна) пространство K(G, n) оказывается Н-пространством и потому представляет некоторую группу H n(X; G) = [X; K(G, n)]. Эта группа называется n-мepной группой когомологий топологического пространства Х с группой коэффициентов G. Она является типичным представителем целого ряда важных кофункторов, к числу которых принадлежит, например, К-функтор KO(X) = [Х, BO], представляемый так называемым бесконечномерным грассманианом BO, группы ориентированных кобордизмов WnX и т.п.
Если G является кольцом, то прямая сумма Н*(Х; G) групп H n(X; G) является алгеброй над G. Более того, эта прямая сумма обладает очень сложной алгебраической структурой, в которую (при G = Zp, где Zp — циклическая группа порядка р) входит действие на Н*(Х; G) некоторой некоммутативной алгебры 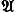 p, называемой алгеброй Стинрода. Сложность этой структуры позволяет, с одной стороны, выработать эффективные (но совсем не простые) методы вычисления групп H n(X; G), а с другой — установить связи между группами H n(X; G) и другими гомотопически инвариантными функторами (например, гомотопическими группами pnX), позволяющие часто в явном виде вычислить и эти функторы.
p, называемой алгеброй Стинрода. Сложность этой структуры позволяет, с одной стороны, выработать эффективные (но совсем не простые) методы вычисления групп H n(X; G), а с другой — установить связи между группами H n(X; G) и другими гомотопически инвариантными функторами (например, гомотопическими группами pnX), позволяющие часто в явном виде вычислить и эти функторы.
Исторически группам когомологий предшествовали так называемые группы гомологий Hn(X; G), являющиеся гомотопическими группами pnM(X, G) некоторого клеточного пространства M(X, G), однозначно строящегося по клеточному пространству Х и группе G. Группы гомологий и когомологий в определённом смысле двойственны друг другу, и их теории по существу равносильны. Однако алгебраическая структура, имеющаяся в группах гомологий, менее привычна (например, эти группы составляют не алгебру, а так называемую коалгебру), и поэтому в вычислениях обычно пользуются группами когомологий. Вместе с тем в некоторых вопросах группы гомологий оказываются более удобными, поэтому они также изучаются. Часть алгебраических Топология, занимающаяся изучением (и применением) групп гомологий и когомологий, называется теорией гомологий.
Перенесение результатов алгебраических Топология на пространства более общие, чем клеточные пространства, составляет предмет так называемой общей алгебраической Топология В частности, общая теория гомологий изучает группы гомологий и когомологий произвольных топологических пространств и их применения. Оказывается, что вне класса компактных клеточных пространств различные подходы к построению этих групп приводят, вообще говоря, к различным результатам, так что для неклеточных топологических пространств возникает целый ряд различных групп гомологий и когомологий. Основное применение общая теория гомологий находит в теории размерности и в теории так называемых законов двойственности (описывающих взаимоотношения между топологическими свойствами двух дополнительных подмножеств топологического пространства), и её развитие было во многом стимулировано нуждами этих теорий.
Топология (от греч. tоpos — место и ¼логия) — часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных подходов к её изучению привели к распадению единой Т. на ряд отделов («общая Т.», «алгебраическая Т.» и др.), отличающихся друг от друга по предмету и методу изучения и фактически весьма мало между собой связанных.
I. Общая топология2. Равномерная топология
3. Алгебраическая топология
4. Кусочно-линейная топология
5. Топология многообразий
6. Основные этапы развития топологии
|
Так же Вы можете узнать о... Сольферино (Solferino), населённый пункт юго-западнее Вероны (провинция Мантуя), в районе которого 24 июня 1859 произошло сражение во время австро-итало французской войны 1859. Таймыр (озеро) Таймыр, Таймырское озеро, озеро на полуострове Таймыр (Красноярский край РСФСР). Трубецкой Николай Сергеевич, князь (16.4.1890, Москва, — 25. Фитопланктон (от фито... и планктон), совокупность растительных организмов, населяющих толщу воды морских и пресных водоёмов и пассивно переносимых течением. Цементация (в строительстве) Цементация в строительстве, закрепление грунтов, горных пород, каменных и бетонных кладок путём нагнетания в пустоты, трещины и поры жидкого цементного раствора или цементной суспензии. Шпольский Эдуард Владимирович [11(23).9.1892, Воронеж, — 21. Янсон Юлий Эдуардович [15(27).10.1835, Киев, — 31. Аниматизм (от лат. animatus — одушевлённый), вера в безличную одушевлённость природы или отдельных её частей и явлений, характерная черта первобытных религий. Басилан (Basilan), город в южной части Филиппин, в провинции Замбоанга-Сур на острове . Бричаны, посёлок городского типа, центр Бричанского района Молдавской ССР, в 16 км от ж. Висциновое масло, минеральное масло, применяемое в воздушных фильтрах вентиляционных установок для очистки воздуха. |
|