Топология 4. Кусочно-линейная топология
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ТОА |
| ТОБ |
| ТОВ |
| ТОГ |
| ТОД |
| ТОЁ |
| ТОЖ |
| ТОЗ |
| ТОИ |
| ТОЙ |
| ТОК |
| ТОЛ |
| ТОМ |
| ТОН |
| ТОО |
| ТОП |
| ТОР |
| ТОС |
| ТОТ |
| ТОУ |
| ТОФ |
| ТОХ |
| ТОЦ |
| ТОЧ |
| ТОШ |
| ТОЩ |
| ТОЯ |
4. Кусочно-линейная топология
Подмножество Р Î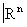 называется конусом с вершиной а и основанием В, если каждая его точка принадлежит единственному отрезку вида ab, где bÎВ. Подмножество ХÎ
называется конусом с вершиной а и основанием В, если каждая его точка принадлежит единственному отрезку вида ab, где bÎВ. Подмножество ХÎ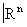 называется полиэдром, если любая его точка обладает в Х окрестностью, замыкание которой является конусом с компактным основанием. Непрерывное отображение f : X®Y полиэдров называется кусочно-линейным, если оно линейно на лучах каждой конической окрестности любой точки хÎX. Взаимно однозначное кусочно-линейное отображение, обратное к которому также кусочно-линейно, называется кусочно-линейным изоморфизмом. Предметом кусочно-линейной Топология является изучение полиэдров и их кусочно-линейных отображений. В кусочно-линейной Топология полиэдры считаются одинаковыми, если они кусочно-линейно изоморфны.
называется полиэдром, если любая его точка обладает в Х окрестностью, замыкание которой является конусом с компактным основанием. Непрерывное отображение f : X®Y полиэдров называется кусочно-линейным, если оно линейно на лучах каждой конической окрестности любой точки хÎX. Взаимно однозначное кусочно-линейное отображение, обратное к которому также кусочно-линейно, называется кусочно-линейным изоморфизмом. Предметом кусочно-линейной Топология является изучение полиэдров и их кусочно-линейных отображений. В кусочно-линейной Топология полиэдры считаются одинаковыми, если они кусочно-линейно изоморфны.
Подмножество ХÎ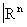 тогда и только тогда является (компактным) полиэдром, когда оно представляет собой объединение (конечного) семейства выпуклых многогранников. Любой полиэдр может быть представлен в виде объединения симплексов, пересекающихся только по целым граням. Такое представление называют триангуляцией полиэдра. Каждая триангуляция однозначно определена её симплициальной схемой, то есть множеством всех её вершин, в котором отмечены подмножества, являющиеся множествами вершин симплексов. Поэтому вместо полиэдров можно рассматривать лишь симп-лициальные схемы их триангуляций. Например, по симплициальной схеме можно вычислять группы гомологий и когомологий. Это делается следующим образом:
тогда и только тогда является (компактным) полиэдром, когда оно представляет собой объединение (конечного) семейства выпуклых многогранников. Любой полиэдр может быть представлен в виде объединения симплексов, пересекающихся только по целым граням. Такое представление называют триангуляцией полиэдра. Каждая триангуляция однозначно определена её симплициальной схемой, то есть множеством всех её вершин, в котором отмечены подмножества, являющиеся множествами вершин симплексов. Поэтому вместо полиэдров можно рассматривать лишь симп-лициальные схемы их триангуляций. Например, по симплициальной схеме можно вычислять группы гомологий и когомологий. Это делается следующим образом:
а) симплекс, вершины которого определённым образом упорядочены, называется упорядоченным симплексом данной триангуляции (или симплициальной схемы) К; формальные линейные комбинации упорядоченных симплексов данной размерности n с коэффициентами из данной группы G называются n-мepными цепями; все они естественным образом составляют группу, которая обозначается символом C n(K; G);
б) выбросив из упорядоченного n-мерного симплекса s вершину с номером i, 0 £ i £ n, получим упорядоченный (n—1)-мерный симплекс, который обозначается символом s(i); цепь 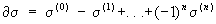 называется границей s; по линейности отображение
называется границей s; по линейности отображение 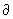 распространяется до гомоморфизма
распространяется до гомоморфизма 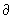 : Cn(K; G)®Cn-1(K; G);
: Cn(K; G)®Cn-1(K; G);
в) цепи с, для которых 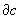 = 0, называются циклами, они составляют группу циклов Zn(K; G);
= 0, называются циклами, они составляют группу циклов Zn(K; G);
г) цепи вида 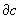 называются границами, они составляют группу границ Bn(K; G);
называются границами, они составляют группу границ Bn(K; G);
д) доказывается, что Bn(K; G)ÌZn(K; G) (граница является циклом); поэтому определена факторгруппа
Hn(K; G)=Zn(K; G)/ Bn(K; G).
Оказывается, что группа Hn(K; G) изоморфна группе гомологий Hn(X; G) полиэдра X, триангуляцией которого является К. Аналогичная конструкция, в которой исходят не из цепей, а из коцепей (произвольных функций, определённых на множестве всех упорядоченных симплексов и принимающих значения в G ), даёт группы когомологий.
С этой конструкции, изложенной здесь в несколько модифицированной форме, и началось по существу становление алгебраической Топология В первоначальной конструкции рассматривались так называемые ориентированные симплексы (классы упорядоченных симплексов, отличающихся чётными перестановками вершин). Эта конструкция развита и обобщена в самых разнообразных направлениях. В частности, её алгебраические аспекты дали начало так называемой гомологической алгебре.
Самым общим образом симплициальную схему можно определить как множество, в котором отмечены некоторые конечные подмножества («симплексы»), причём требуется, чтобы любое подмножество симплекса было снова симплексом. Такая симплициальная схема является симплициальной схемой триангуляции некоторого полиэдра тогда и только тогда, когда число элементов произвольного отмеченного подмножества не превосходит некоторого фиксированного числа. Впрочем, понятие полиэдра можно обобщить (получив так называемые «бесконечномерные полиэдры»), и тогда уже любая симплициальная схема будет схемой триангуляции некоторого полиэдра (называемого её геометрической реализацией).
Произвольному открытому покрытию {Ua} каждого топологического пространства Х можно сопоставить симплициальную схему, вершинами которой являются элементы Ua покрытия и подмножество которой тогда и только тогда отмечено, когда элементы покрытия, составляющие это подмножество, имеют непустое пересечение. Эта симплициальная схема (и соответствующий полиэдр) называемому нервом покрытия. Нервы всевозможных покрытий в определённом смысле аппроксимируют пространство Х и, исходя из их групп гомологий и когомологий, можно посредством соответствующего предельного перехода получать группы гомологий и когомологий самого X. Эта идея лежит в основе почти всех конструкций общей теории гомологий. Аппроксимация топологического пространства нервами его открытых покрытий играет важную роль и в общей Топология
Топология (от греч. tоpos — место и ¼логия) — часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных подходов к её изучению привели к распадению единой Т. на ряд отделов («общая Т.», «алгебраическая Т.» и др.), отличающихся друг от друга по предмету и методу изучения и фактически весьма мало между собой связанных.
I. Общая топология2. Равномерная топология
3. Алгебраическая топология
4. Кусочно-линейная топология
5. Топология многообразий
6. Основные этапы развития топологии
|
Так же Вы можете узнать о... Генеральный план, генплан, 1) Г. п. развития города — научно обоснованный перспективный план развития города (применительно к старому городу — его реконструкции и дальнейшего развития). «Гудок» (большевист. газета) «Гудок», легальная еженедельная большевистская газета, издававшаяся профсоюзом бакинских нефтепромышленных рабочих в 1907—08. Доннер Отто Доннер (Donner) Отто (15.12.1835, Коккола, — 1909), финский лингвист-угрофиновед. Золотой Берег (англ. Gold Coast), 1) побережье Гвинейского залива на территории Ганы. Каляев Иван Платонович [24.6(6.7).1877, Варшава, — 10(23). Клюзере Гюстав Поль Клюзере (Cluseret) Гюстав Поль (13.6.1823, Париж, — 23. Кремази Октав Жозеф Кремази (Crémazie) Октав Жозеф (16. Ли Жу-чжэнь (второе имя Сунши) (около 1763 — 1830), китайский писатель и филолог. Марха (река в Якутской АССР, лев. приток р. Лена) Марха, река в Якутской АССР, левый приток реки Лена. Монтесума, Моктесума, 1) М. (1390 — около 1469), вождь ацтеков. Нитчатые бактерии, образующие нити длиной до 1 см, разделённые перегородками на клетки цилиндрической формы (0,5—2 мкм х 2—5 мкм). |
|