Топология 5. Топология многообразий
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ТОА |
| ТОБ |
| ТОВ |
| ТОГ |
| ТОД |
| ТОЁ |
| ТОЖ |
| ТОЗ |
| ТОИ |
| ТОЙ |
| ТОК |
| ТОЛ |
| ТОМ |
| ТОН |
| ТОО |
| ТОП |
| ТОР |
| ТОС |
| ТОТ |
| ТОУ |
| ТОФ |
| ТОХ |
| ТОЦ |
| ТОЧ |
| ТОШ |
| ТОЩ |
| ТОЯ |
5. Топология многообразий
Хаусдорфово паракомпактное топологическое пространство называется n-мерным топологическим многообразием, если оно «локально евклидово», то есть если каждая его точка обладает окрестностью (называемой координатной окрестностью, или картой), гомеоморфной топологическому пространству 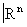 . В этой окрестности точки задаются n числами x1, …, xn, называемыми локальными координатами. В пересечении двух карт соответствующие локальные координаты выражаются друг через друга посредством некоторых функций, называемых функциями перехода. Эти функции задают гомеоморфизм открытых множеств в
. В этой окрестности точки задаются n числами x1, …, xn, называемыми локальными координатами. В пересечении двух карт соответствующие локальные координаты выражаются друг через друга посредством некоторых функций, называемых функциями перехода. Эти функции задают гомеоморфизм открытых множеств в 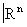 , называются гомеоморфизмом перехода.
, называются гомеоморфизмом перехода.
Условимся произвольный гомеоморфизм между открытыми множествами из 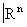 называть t-гомеоморфизмом. Гомеоморфизм, являющийся кусочно-линейным изоморфизмом, будем называть p-гомеоморфизмом, а если он выражается гладкими (дифференцируемыми любое число раз) функциями, — s-гомеоморфизмом.
называть t-гомеоморфизмом. Гомеоморфизм, являющийся кусочно-линейным изоморфизмом, будем называть p-гомеоморфизмом, а если он выражается гладкими (дифференцируемыми любое число раз) функциями, — s-гомеоморфизмом.
Пусть a= t, p или s. Топологическое многообразие называется a-многообразием, если выбрано такое его покрытие картами, что гомеоморфизмы перехода для любых его двух (пересекающихся) карт являются a-гомеоморфизмами. Такое покрытие задаёт a-структуру на топологическом многообразии X. Таким образом, t-многообразие — это просто любое топологическое многообразие, p-многообразия называются кусочно-линейными многообразиями. Каждое кусочно-линейное многообразие является полиэдром. В классе всех полиэдров n-мерные кусочно-линейные многообразия характеризуются тем, что любая их точка обладает окрестностью, кусочно-линейно изоморфной n-мерному кубу. s-многообразия называются гладкими (или дифференцируемыми) многообразиями. a-отображением a-многообразия называются называется при a = t произвольное непрерывное отображение, при a = s — произвольное кусочно-линейное отображение, при a = s — произвольное гладкое отображение, то есть непрерывное отображение, записывающееся в локальных координатах гладкими функциями. Взаимно однозначное a-отображение, обратное к которому также является a-отображением, называется a-гомеоморфизмом (при a = s также диффеоморфизмом), a-многообразия Х и Y называются a-гомеоморфными (при a = s — диффеоморфными), если существует хотя бы один a-гомеоморфизм X ® Y. Предметом теории a-многообразий является изучение a-многообразий и их a-отображений; при этом a-гомеоморфные a-многообразия считаются одинаковыми. Теория s-многообразий является частью кусочно-линейной Топология Теория s-многообразий называется также гладкой Топология
Основной метод современной теории многообразий состоит в сведении её задач к проблемам алгебраических Топология для некоторых нужным образом сконструированных топологических пространств. Эта тесная связь теории многообразий с алгебраической Топология позволила, с одной стороны, решить много трудных геометрических проблем, а с другой — резко стимулировала развитие самой алгебраической Топология
Примерами гладких многообразий являются n-мерные поверхности в 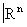 , не имеющие особых точек. Оказывается (теорема вложения), что любое гладкое многообразие диффеоморфно такой поверхности (при N ³ 2n + 1). Аналогичный результат верен и при a=t, p.
, не имеющие особых точек. Оказывается (теорема вложения), что любое гладкое многообразие диффеоморфно такой поверхности (при N ³ 2n + 1). Аналогичный результат верен и при a=t, p.
Каждое p-многообразие является t-многообразием. Оказывается, что на любом s-многообразии можно некоторым естественным образом ввести p-структуру (которая называется обычно у айтхедовской триангуляцией). Можно сказать, что любое a-многообразие, где a = p или s, является a’-многообразием, где a’ = t или p. Ответ на обратный вопрос: на каких a’-многообразиях можно ввести a-структуру (такое a’-многообразие при a’ = p называется сглаживаемым, а при a’ = t — триангулируемым), а если можно, то сколько? — зависит от размерности n.
Существует только два одномерных топологических многообразия: окружность S1 (компактное многообразие) и прямая линия 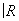 (некомпактное многообразие). Для любого a = p, s на t-многообразиях S1 и
(некомпактное многообразие). Для любого a = p, s на t-многообразиях S1 и 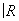 существует единственная a-структура.
существует единственная a-структура.
Аналогично, на любом двумерном топологическом многообразии (поверхности) существует единственная a-структура, и можно легко описать все компактные связные поверхности (некомпактные связные поверхности также могут быть описаны, но ответ получается более сложный). Для того чтобы поверхности были гомеоморфны, достаточно, чтобы они были гомотопически эквивалентны. При этом гомотопический тип любой поверхности однозначно характеризуется её группами гомологий. Существует два типа поверхностей: ориентируемые и неориентируемые. К числу ориентируемых принадлежит сфера S2 и тор T2. Пусть Х и Y — два связных n-мерных a-многообразия. Вырежем в Х и Y по шару (при n = 2 — диску) и склеим получившиеся граничные сферы (при n = 2 — окружности). При соблюдении некоторых само собой разумеющихся предосторожностей в результате снова получим a-многообразие. Оно называется связной суммой a-многообразий Х и Y и обозначается X#Y. Например, T2#T2 имеет вид кренделя. Сфера S n является нулём этого сложения, то есть S n#X = Х для любого X. В частности, S2#T2 = T2. Оказывается, что ориентируемая поверхность гомеоморфна связной сумме вида S2#T2#…#T2, число p слагаемых T2 называется родом поверхности. Для сферы p = 0, для тора p = 1 и т. д. Поверхность рода p можно наглядно представлять себе как сферу, к которой приклеено p «ручек». Каждая неориентируемая поверхность гомеоморфна связной сумме 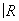 P2# ¼ #
P2# ¼ #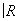 P2 некоторого числа проективных плоскостей
P2 некоторого числа проективных плоскостей 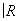 P2. Её можно представлять себе как сферу, к которой приклеено несколько Мебиуса листов.
P2. Её можно представлять себе как сферу, к которой приклеено несколько Мебиуса листов.
На каждом трёхмерном топологическом многообразии при любом a = p, s также существует единственная a-структура и можно описать все гомотопические типы трёхмерных топологических многообразий (однако групп гомологий для этого уже недостаточно). В то же время до сих пор (1976) не описаны все (хотя бы компактные связные) трёхмерные топологические многообразия данного гомотопического типа. Это не сделано даже для односвязных многообразий (все они гомотопически эквивалентны сфере S 3). Гипотеза Пуанкаре утверждает, что любое такое многообразие гомеоморфно S 3.
Для четырёхмерных (компактных и связных) топологических многообразий вопрос о существовании и единственности a-структур (a = p, s) ещё не решен, а их гомотопический тип описан только в предположении односвязности. Справедлив ли для них аналог гипотезы Пуанкаре, неизвестно.
Замечательно, что для компактных и связных топологических многообразий размерности n ³ 5 ситуация оказывается совсем иной: все основные задачи для них можно считать в принципе решенными (точнее, сведёнными к проблемам алгебраической Топология). Любое гладкое многообразие Х вкладывается как гладкая (n-мepная) поверхность в 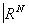 ; и касательные векторы к Х составляют некоторое новое гладкое многообразие TX, которое называется касательным расслоением гладкого многообразия X. Вообще, векторным расслоением над топологическим пространством Х называется топологическое пространство Е, для которого задано такое непрерывное отображение p : Е®Х, что для каждой точки хÎХ прообраз v (слой) является векторным пространством и существует такое открытое покрытие {Ua} пространства X, что для любого a прообраз p—1(Ua) гомеоморфен произведению Ua´
; и касательные векторы к Х составляют некоторое новое гладкое многообразие TX, которое называется касательным расслоением гладкого многообразия X. Вообще, векторным расслоением над топологическим пространством Х называется топологическое пространство Е, для которого задано такое непрерывное отображение p : Е®Х, что для каждой точки хÎХ прообраз v (слой) является векторным пространством и существует такое открытое покрытие {Ua} пространства X, что для любого a прообраз p—1(Ua) гомеоморфен произведению Ua´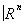 , причём существует гомеоморфизм p—1(Ua) ®Ua´
, причём существует гомеоморфизм p—1(Ua) ®Ua´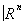 , линейно отображающий каждый слой p—1(x), xÎUa, на векторное пространство {х}´
, линейно отображающий каждый слой p—1(x), xÎUa, на векторное пространство {х}´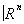 . При Е = TX непрерывное отображение p сопоставляет с каждым касательным вектором точку его касания, так что слоем p—1(x) будет пространство, касательное к Х в точке х. Оказывается, что любое векторное расслоение над компактным пространством Х определяет некоторый элемент группы KO(X). Таким образом, в частности, для любого гладкого, компактного и связного многообразия Х в группе KO(X) определён элемент, соответствующий касательному расслоению. Он называется тангенциальным инвариантом гладкого многообразия X. Имеется аналог этой конструкции для любого a. При a = p роль группы KO(X) играет некоторая другая группа, которая обозначается KPL(X), а при a = t роль этой группы играет группа, обозначаемая KTop(X). Каждое a-многообразие Х определяет в соответствующей группе [КО(Х), KPL(X) или KTop(X)] некоторый элемент, называемый его a-тангенциальным инвариантом. Имеются естественные гомоморфизмы KO(X)®KPL(X)®KTop(X), и оказывается, что на n-мерном (n ³ 5) компактном и связном a'-многообразии X, где a' = t, p, тогда и только тогда можно ввести a-структуру (a = р, если a' = t, и a = s, если a' = p), когда его a'-тангенциальный инвариант лежит в образе соответствующей группы [KPL(X) при a' = t и KO(X) при a' = p]. Число таких структур конечно и равно числу элементов некоторого фактормножества множества [X, Ya], где Ya — некоторое специальным образом сконструированное топологическое пространство (при a = s топологическое пространство Ya обозначается обычно символом PL/O, а при a = p — символом Top/PL). Тем самым вопрос о существовании и единственности a-структуры сводится к некоторой задаче теории гомотопий. Гомотопический тип топологического пространства PL/O довольно сложен и до сих пор (1976) полностью не вычислен; однако известно, что pi(PL/O) = 0 при i £ 6, откуда следует, что любое кусочно-линейное многообразие размерности n £ 7 сглаживаемо, а при n £ 6 единственным образом. Напротив, гомотопический тип топологического пространства Top/PL оказался удивительно простым: это пространство гомотопически эквивалентно K(ℤ2, 3). Следовательно, число кусочно-линейных структур на топологическом многообразии не превосходит числа элементов группы H 3(X, ℤ2). Такие структуры заведомо существуют, если H 4(X, ℤ2) = 0, но при H 4(X, ℤ2) ¹ 0 кусочно-линейной структуры может не существовать.
. При Е = TX непрерывное отображение p сопоставляет с каждым касательным вектором точку его касания, так что слоем p—1(x) будет пространство, касательное к Х в точке х. Оказывается, что любое векторное расслоение над компактным пространством Х определяет некоторый элемент группы KO(X). Таким образом, в частности, для любого гладкого, компактного и связного многообразия Х в группе KO(X) определён элемент, соответствующий касательному расслоению. Он называется тангенциальным инвариантом гладкого многообразия X. Имеется аналог этой конструкции для любого a. При a = p роль группы KO(X) играет некоторая другая группа, которая обозначается KPL(X), а при a = t роль этой группы играет группа, обозначаемая KTop(X). Каждое a-многообразие Х определяет в соответствующей группе [КО(Х), KPL(X) или KTop(X)] некоторый элемент, называемый его a-тангенциальным инвариантом. Имеются естественные гомоморфизмы KO(X)®KPL(X)®KTop(X), и оказывается, что на n-мерном (n ³ 5) компактном и связном a'-многообразии X, где a' = t, p, тогда и только тогда можно ввести a-структуру (a = р, если a' = t, и a = s, если a' = p), когда его a'-тангенциальный инвариант лежит в образе соответствующей группы [KPL(X) при a' = t и KO(X) при a' = p]. Число таких структур конечно и равно числу элементов некоторого фактормножества множества [X, Ya], где Ya — некоторое специальным образом сконструированное топологическое пространство (при a = s топологическое пространство Ya обозначается обычно символом PL/O, а при a = p — символом Top/PL). Тем самым вопрос о существовании и единственности a-структуры сводится к некоторой задаче теории гомотопий. Гомотопический тип топологического пространства PL/O довольно сложен и до сих пор (1976) полностью не вычислен; однако известно, что pi(PL/O) = 0 при i £ 6, откуда следует, что любое кусочно-линейное многообразие размерности n £ 7 сглаживаемо, а при n £ 6 единственным образом. Напротив, гомотопический тип топологического пространства Top/PL оказался удивительно простым: это пространство гомотопически эквивалентно K(ℤ2, 3). Следовательно, число кусочно-линейных структур на топологическом многообразии не превосходит числа элементов группы H 3(X, ℤ2). Такие структуры заведомо существуют, если H 4(X, ℤ2) = 0, но при H 4(X, ℤ2) ¹ 0 кусочно-линейной структуры может не существовать.
В частности, на сфере S n существует единственная кусочно-линейная структура. Гладких структур на сфере S n может быть много, например, на S 7 существует 28 различных гладких структур. На торе T n (топологических произведении n экземпляров окружности S 1) существует при n ³ 5 много различных кусочно-линейных структур, которые все допускают гладкую структуру. Таким образом, начиная с размерности 5, существуют гомеоморфные, но не диффеоморфные гладкие многообразия; сферы с таким свойством существуют, начиная с размерности 7.
Задачу описания (с точностью до a-гомеоморфизма) всех n-мерpных (n ³ 5) связных компактных a-многообразий естественно решать в два этапа: искать условия гомотопической эквивалентности a-многообразий и условия a-гомеоморфности гомотопически эквивалентных a-многообразий. Первая задача относится к гомотопической Топология и в её рамках может считаться полностью решенной. Вторая задача также по существу полностью решена (во всяком случае для односвязных a-многообразий). Основой её решения является перенос в высшие размерности техники «разложения на ручки». С помощью этой техники удаётся, например, доказать для n-мерных (n ³ 5) топологических многообразий гипотезу Пуанкаре (связное компактное топологическое многообразие, гомотопически эквивалентное сфере, гомеоморфно ей).
Наряду с a-многообразиями можно рассматривать так называемые a-многообразия с краем; они характеризуются тем, что окрестности некоторых их точек (составляющих край) a-гомеоморфны полупространству Xn ³ 0 пространства 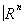 . Край является (n—1)-мерным a-многообразием (вообще говоря, несвязным). Два n-мерных компактных a-многообразия Х и Y называются (ко) бордантными, если существует такое (n+1)-мерное компактное a-многообразие с краем W, что его край является объединением непересекающихся гладких многообразий, a-гомеоморфных Х и У. Если отображения вложения X ® W и Y ® W являются гомотопическими эквивалентностями, то гладкие многообразия называются h-кобордантными. Методами разложения на ручки удаётся доказать, что при n ³ 5 односвязные компактные a-многоооразия a-гомеоморфны, если они h-кобордантны. Эта теорема о h-кобордизме доставляет сильнейший способ установления a-гомеоморфности a-многообразий (в частности, гипотеза Пуанкаре является её следствием). Аналогичный, но более сложный результат имеет место и для неодносвязных a-многообразий.
. Край является (n—1)-мерным a-многообразием (вообще говоря, несвязным). Два n-мерных компактных a-многообразия Х и Y называются (ко) бордантными, если существует такое (n+1)-мерное компактное a-многообразие с краем W, что его край является объединением непересекающихся гладких многообразий, a-гомеоморфных Х и У. Если отображения вложения X ® W и Y ® W являются гомотопическими эквивалентностями, то гладкие многообразия называются h-кобордантными. Методами разложения на ручки удаётся доказать, что при n ³ 5 односвязные компактные a-многоооразия a-гомеоморфны, если они h-кобордантны. Эта теорема о h-кобордизме доставляет сильнейший способ установления a-гомеоморфности a-многообразий (в частности, гипотеза Пуанкаре является её следствием). Аналогичный, но более сложный результат имеет место и для неодносвязных a-многообразий.
Совокупность 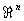 классов кобордантных компактных a-многообразий является по отношению к операции связной суммы коммутативной группой. Нулём этой группы служит класс a-многообразий, являющихся краями, то есть кобордантных нулю. Оказывается, что эта группа при a = s изоморфна гомотопической группе p2n+1MO (n+1) некоторого специально сконструированного топологического пространства MO (n+1), называется пространством Тома. Аналогичный результат имеет место и при a = p, t. Поэтому методы алгебраической Топология позволяют в принципе вычислить группу
классов кобордантных компактных a-многообразий является по отношению к операции связной суммы коммутативной группой. Нулём этой группы служит класс a-многообразий, являющихся краями, то есть кобордантных нулю. Оказывается, что эта группа при a = s изоморфна гомотопической группе p2n+1MO (n+1) некоторого специально сконструированного топологического пространства MO (n+1), называется пространством Тома. Аналогичный результат имеет место и при a = p, t. Поэтому методы алгебраической Топология позволяют в принципе вычислить группу 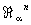 . В частности, оказывается, что группа
. В частности, оказывается, что группа 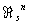 является прямой суммой групп ℤ2 в количестве, равном числу разбиений числа n на слагаемые, отличные от чисел вида 2m—1. Например,
является прямой суммой групп ℤ2 в количестве, равном числу разбиений числа n на слагаемые, отличные от чисел вида 2m—1. Например, 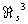 = 0 (так что каждое трёхмерное компактное гладкое многообразие является краем). Напротив,
= 0 (так что каждое трёхмерное компактное гладкое многообразие является краем). Напротив, 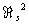 = ℤ2, так что существуют поверхности, кобордантные друг другу и не кобордантные нулю; такой поверхностью, например, является проективная плоскость
= ℤ2, так что существуют поверхности, кобордантные друг другу и не кобордантные нулю; такой поверхностью, например, является проективная плоскость  P 2.
P 2.
М. М. Постников.
Топология (от греч. tоpos — место и ¼логия) — часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных подходов к её изучению привели к распадению единой Т. на ряд отделов («общая Т.», «алгебраическая Т.» и др.), отличающихся друг от друга по предмету и методу изучения и фактически весьма мало между собой связанных.
I. Общая топология2. Равномерная топология
3. Алгебраическая топология
4. Кусочно-линейная топология
5. Топология многообразий
6. Основные этапы развития топологии
|
Так же Вы можете узнать о... Палеоантропы (от палео... и греч. anthropos — человек), обобщённое (не систематическое) название ископаемых людей, обитавших в Азии, Африке и Европе 250—35 тыс. Полёвки (Microtinae), подсемейство грызунов семейства хомяков; некоторые зоологи выделяют семейства полёвковых (или полёвок). «Радянське лiтературознавство» («Советское литературоведение»), советский журнал теории, истории литературы и литературной критики. Сандал (озеро в Карельской АССР) Сандал, озеро на Ю. Карельской АССР. Площадь 152 км2. «Совет Тожикистони» («Советский Таджикистан»), ежедневная республиканская газета Таджикской ССР на узбекском языке. Сюй Бэй-хун, Жю Пэон (19.6. 1895, уезд Исин, провинция Цзянсу, — 26. Туба (река) Туба, река в Красноярском крае РСФСР, правый приток р. Формен Лайонел Формен (Forman) Лайонел (25.12.1927, Йоханнесбург, – 19. «Чайка», легковой автомобиль с большим литражом двигателя, выпускаемый Горьковским автомобильным заводом с 1950 (модель ГАЗ-13 с 1959, ГАЗ-14 с 1977). Эксплантация (от экс... и лат. planto — caжаю) (биол. Азотистоводородная кислота, азоимид, HN3, соединение азота с водородом, бесцветная летучая жидкость с резким запахом. |
|