Топология I. Общая топология
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ТОА |
| ТОБ |
| ТОВ |
| ТОГ |
| ТОД |
| ТОЁ |
| ТОЖ |
| ТОЗ |
| ТОИ |
| ТОЙ |
| ТОК |
| ТОЛ |
| ТОМ |
| ТОН |
| ТОО |
| ТОП |
| ТОР |
| ТОС |
| ТОТ |
| ТОУ |
| ТОФ |
| ТОХ |
| ТОЦ |
| ТОЧ |
| ТОШ |
| ТОЩ |
| ТОЯ |
I. Общая топология
Часть Топология, ориентированная на аксиоматическое изучение непрерывности, называется общей Топология Наряду с алгеброй общая Топология составляет основу современного теоретико-множественного метода в математике.
Аксиоматически непрерывность можно определить многими (вообще говоря, неравносильными) способами. Общепринята аксиоматика, основывающаяся на понятии открытого множества. Топологической структурой, или топологией, на множестве Х называют такое семейство его подмножеств, называемых открытыми множествами, что: 1) пустое множество Æ и всё Х открыты; 2) объединение любого числа и пересечение конечного числа открытых множеств открыто. Множество, на котором задана топологическая структура, называют топологическим пространством. В топологическом пространстве Х можно определить все основные понятия элементарного анализа, связанные с непрерывностью. Например, окрестностью точки x Î X называют произвольное открытое множество, содержащее эту точку; множество A Ì X называют замкнутым, если его дополнение Х \ А открыто; замыканием множества А называют наименьшее замкнутое множество, содержащее A; если это замыкание совпадает с X, то А называют всюду плотным в Х и т.д.
По определению, Æ и Х являются одновременно замкнутыми и открытыми множествами. Если в Х нет других множеств, одновременно замкнутых и открытых, то топологическое пространство Х называют связным. Наглядно связное пространство состоит из одного «куска», а несвязное — из нескольких.
Любое подмножество А топологического пространства Х обладает естественной топологической структурой, состоящей из пересечений с А открытых множеств из X. Снабженное этой структурой А называют подпространством пространства X. Каждое метрическое пространство становится топологическим, если за его открытые множества принять множества, содержащие вместе с произвольной точкой некоторую её e-окрестность (шар радиуса e с центром в этой точке). В частности, любое подмножество n-мерного евклидова пространства 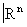 является топологическим пространством. Теория таких пространств (под названием «геометрической Топология») и теория метрических пространств включаются по традиции в общую Топология
является топологическим пространством. Теория таких пространств (под названием «геометрической Топология») и теория метрических пространств включаются по традиции в общую Топология
Геометрическая Топология довольно четко распадается на две части: изучение подмножеств 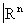 произвольной сложности, подчинённых тем или иным ограничениям общего характера (примером является так называемая теория континуумов, то есть связных ограниченных замкнутых множеств), и изучение способов, какими в
произвольной сложности, подчинённых тем или иным ограничениям общего характера (примером является так называемая теория континуумов, то есть связных ограниченных замкнутых множеств), и изучение способов, какими в 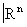 могут быть вложены такие простые топологические пространства, как сфера, шар и т.п. (вложения в
могут быть вложены такие простые топологические пространства, как сфера, шар и т.п. (вложения в 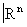 , например, сфер могут быть очень сложно устроенными).
, например, сфер могут быть очень сложно устроенными).
Открытым покрытием топологического пространства Х называют семейство его открытых множеств, объединением которого является всё X. Топологическое пространство Х называют компактным (в другой терминологии —бикомпактным), если любое его открытое покрытие содержит конечное число элементов, также образующих покрытие. Классическая теорема Гейне — Бореля утверждает, что любое ограниченное замкнутое подмножество 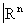 компактно. Оказывается, что все основные теоремы элементарного анализа об ограниченных замкнутых множествах (например, теорема Вейерштрасса о том, что на таком множестве непрерывная функция достигает своего наибольшего значения) справедливы для любых компактных топологических пространств. Это определяет фундаментальную роль, которую играют компактные пространства в современной математике (особенно в связи с теоремами существования). Выделение класса компактных топологических пространств явилось одним из крупнейших достижений обшей Топология, имеющих общематематическое значение.
компактно. Оказывается, что все основные теоремы элементарного анализа об ограниченных замкнутых множествах (например, теорема Вейерштрасса о том, что на таком множестве непрерывная функция достигает своего наибольшего значения) справедливы для любых компактных топологических пространств. Это определяет фундаментальную роль, которую играют компактные пространства в современной математике (особенно в связи с теоремами существования). Выделение класса компактных топологических пространств явилось одним из крупнейших достижений обшей Топология, имеющих общематематическое значение.
Открытое покрытие {Vb} называют вписанным в покрытие {Ua}, если для любого b существует a такое, что VbÌUa. Покрытие {Vb} называют локально конечным, если каждая точка хÎХ обладает окрестностью, пересекающейся только с конечным числом элементов этого покрытия. Топологическое пространство называют паракомпактным, если в любое его открытое покрытие можно вписать локально конечное покрытие. Класс паракомпактных пространств является примером классов топологических пространств, получающихся наложением так называемых условий типа компактности. Этот класс очень широк, в частности он содержит все метризуемые топологические пространства, то есть пространства X, в которых можно ввести такую метрику r, что Топология, порожденная r в X, совпадает с Топология, заданной в X.
Кратностью открытого покрытия называют наибольшее число k такое, что найдётся k его элементов, имеющих непустое пересечение. Наименьшее число n, обладающее тем свойством, что в любое конечное открытое покрытие топологического пространства Х можно вписать открытое покрытие кратности £n + 1, обозначается символом dimХ и называется размерностью X. Это название оправдано тем, что в элементарно-геометрических ситуациях dimХ совпадает с обычно понимаемой размерностью, например dim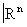 =n. Возможны и др. числовые функции топологического пространства X, отличающиеся от dimX, но в простейших случаях совпадающие с dimX. Их изучение составляет предмет общей теории размерности — наиболее геометрически ориентированной части общей Топология Только в рамках этой теории удаётся, например, дать чёткое и достаточно общее определение интуитивного понятия геометрической фигуры и, в частности, понятия линии, поверхности и т.п.
=n. Возможны и др. числовые функции топологического пространства X, отличающиеся от dimX, но в простейших случаях совпадающие с dimX. Их изучение составляет предмет общей теории размерности — наиболее геометрически ориентированной части общей Топология Только в рамках этой теории удаётся, например, дать чёткое и достаточно общее определение интуитивного понятия геометрической фигуры и, в частности, понятия линии, поверхности и т.п.
Важные классы топологических пространств получаются наложением так называемых аксиом отделимости. Примером является так называемая аксиома Хаусдорфа, или аксиома T2, требующая, чтобы любые две различные точки обладали непересекающимися окрестностями. Топологическое пространство, удовлетворяющее этой аксиоме, называется хаусдорфовым, или отделимым. Некоторое время в математической практике встречались почти исключительно хаусдорфовы пространства (например, любое метрическое пространство хаусдорфово). Однако роль нехаусдорфовых топологических пространств в анализе и геометрии постоянно растет.
Топологические пространства, являющиеся подпространствами хаусдорфовых (би) компактных пространств, называются вполне регулярными или тихоновскими. Их тоже можно охарактеризовать некоторой аксиомой отделимости, а именно: аксиомой, требующей, чтобы для любой точки x0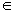 Х и любого не содержащего её замкнутого множества F
Х и любого не содержащего её замкнутого множества F 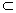 Х существовала непрерывная функция g : Х ® [0, 1], равная нулю в x0 и единице на F.
Х существовала непрерывная функция g : Х ® [0, 1], равная нулю в x0 и единице на F.
Топологические пространства, являющиеся открытыми подпространствами хаусдорфовых компактных, называются локально компактными пространствами. Они характеризуются (в классе хаусдорфовых пространств) тем, что каждая их точка обладает окрестностью с компактным замыканием (пример: евклидово пространство). Любое такое пространство дополняется одной точкой до компактного (пример: присоединением одной точки из плоскости получается сфера комплексного переменного, а из 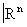 — сфера S n).
— сфера S n).
Отображение f : X ® Y топологическое пространства Х в топологическое пространство Y называют непрерывным отображением, если для любого открытого множества VÌY множество f—1(V) открыто в X. Непрерывное отображение называют гомеоморфизмом, если оно взаимно однозначно и обратное отображение f—1: Y ® X непрерывно. Такое отображение устанавливает взаимно однозначное соответствие между открытыми множествами топологических пространств Х и Y, перестановочное с операциями объединения и пересечения множеств. Поэтому все топологические свойства (то есть свойства, формулируемые в терминах открытых множеств) этих пространств одни и те же, и с топологической точки зрения гомеоморфные топологические пространства (то есть пространства, для которых существует хотя бы один гомеоморфизм Х ®Y) следует считать одинаковыми (подобно тому как в евклидовой геометрии одинаковыми считаются фигуры, которые можно совместить движением). Например, гомеоморфны («топологически одинаковы») окружность и граница квадрата, шестиугольника и т.п. Вообще любые две простые (не имеющие двойных точек) замкнутые линии гомеоморфны. Напротив, окружность не гомеоморфна прямой (ибо удаление точки не нарушает связности окружности, но нарушает связность прямой; по той же причине прямая не гомеоморфна плоскости, а окружность не гомеоморфна «восьмёрке»). Окружность не гомеоморфна также и плоскости (выкиньте не одну, а две точки).
Пусть {Хa} — произвольное семейство топологических пространств. Рассмотрим множество Х всех семейств вида {хa}, где xa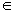 Xa (прямое произведение множеств Xa). Для любого a формула
Xa (прямое произведение множеств Xa). Для любого a формула 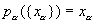 определяет некоторое отображение
определяет некоторое отображение 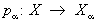 (называется проекцией). Вообще говоря, в Х можно ввести много топологических структур, относительно которых все отображения pa непрерывны. Среди этих структур существует наименьшая (то есть содержащаяся в любой такой структуре). Снабженное этой топологической структурой множество Х называется топологическим произведением топологических пространств Хa и обозначается символом ПХa (а в случае конечного числа сомножителей — символом X1´ ... ´Xn). В явном виде открытые множества пространства Х можно описать как объединения конечных пересечений всех множеств вида
(называется проекцией). Вообще говоря, в Х можно ввести много топологических структур, относительно которых все отображения pa непрерывны. Среди этих структур существует наименьшая (то есть содержащаяся в любой такой структуре). Снабженное этой топологической структурой множество Х называется топологическим произведением топологических пространств Хa и обозначается символом ПХa (а в случае конечного числа сомножителей — символом X1´ ... ´Xn). В явном виде открытые множества пространства Х можно описать как объединения конечных пересечений всех множеств вида 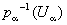 , где Ua открыто в Xa. Топологическое пространство Х обладает следующим замечательным свойством универсальности, однозначно (с точностью до гомеоморфизма) его характеризующим: для любого семейства непрерывных отображений fa : Y®Xa существует единственное непрерывное отображение f : Y®X, для которого
, где Ua открыто в Xa. Топологическое пространство Х обладает следующим замечательным свойством универсальности, однозначно (с точностью до гомеоморфизма) его характеризующим: для любого семейства непрерывных отображений fa : Y®Xa существует единственное непрерывное отображение f : Y®X, для которого 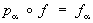 при всех a. Пространство
при всех a. Пространство 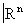 является топологическим произведением n экземпляров числовой прямой. Одной из важнейших теорем общей Топология является утверждение о том, что топологическое произведение компактных топологических пространств компактно.
является топологическим произведением n экземпляров числовой прямой. Одной из важнейших теорем общей Топология является утверждение о том, что топологическое произведение компактных топологических пространств компактно.
Если Х — топологическое пространство, а Y — произвольное множество и если задано отображение p : X®Y пространства Х на множество Y (например, если Y является фактормножеством Х по некоторому отношению эквивалентности, а p представляет собой естественную проекцию, сопоставляющую с каждым элементом хÎ Х его класс эквивалентности), то можно ставить вопрос о введении в Y топологической структуры, относительно которой отображение p непрерывно. Наиболее «богатую» (открытыми множествами) такую структуру получают, полагая открытыми множествами в Y все те множества VÌY, для которых множество f‑1(V) ÌХ открыто в X. Снабженное этой топологической структурой множество Y называется факторпространством топологического пространства Х (по отношению к p ). Оно обладает тем свойством, что произвольное отображение f : Y®Z тогда и только тогда непрерывно, когда непрерывно отображение 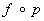 : X®Z. Непрерывное отображение p : X®Y называется факторным, если топологическое пространство Y является по отношению к p факторпространством топологического пространства X. Непрерывное отображение p : X®Y называется открытым, если для любого открытого множества UÌХ множество p(U) открыто в Y, и замкнутым, если для любого замкнутого множества FÌХ множество p(F) замкнуто в Y. Как открытые, так и замкнутые непрерывные отображения f : Х®Y, для которых f(X) = Y, являются факторными.
: X®Z. Непрерывное отображение p : X®Y называется факторным, если топологическое пространство Y является по отношению к p факторпространством топологического пространства X. Непрерывное отображение p : X®Y называется открытым, если для любого открытого множества UÌХ множество p(U) открыто в Y, и замкнутым, если для любого замкнутого множества FÌХ множество p(F) замкнуто в Y. Как открытые, так и замкнутые непрерывные отображения f : Х®Y, для которых f(X) = Y, являются факторными.
Пусть Х — топологическое пространство, А — его подпространство и f : A®Y — непрерывное отображение. Предполагая топологические пространства Х и Y непересекающимися, введём в их объединении ХÈY топологическую структуру, считая открытыми множествами объединения открытых множеств из Х и Y. Далее, введём в пространстве ХÈY наименьшее отношение эквивалентности, в котором a ~ f(a) для любой точки aÎ А. Соответствующее факторпространство обозначается символом XÈfY, и о нём говорят, что оно получено приклеиванием топологического пространства Х к топологическому пространству Y по А посредством непрерывного отображения f. Эта простая и наглядная операция оказывается очень важной, так как позволяет получать из сравнительно простых топологических пространств более сложные. Если Y состоит из одной точки, то пространство ХÈfY обозначается символом Х/А и о нём говорят, что оно получено из Х стягиванием А в точку. Например, если Х — диск, а А — его граничная окружность, то Х/А гомеоморфно сфере.
Топология (от греч. tоpos — место и ¼логия) — часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных подходов к её изучению привели к распадению единой Т. на ряд отделов («общая Т.», «алгебраическая Т.» и др.), отличающихся друг от друга по предмету и методу изучения и фактически весьма мало между собой связанных.
I. Общая топология2. Равномерная топология
3. Алгебраическая топология
4. Кусочно-линейная топология
5. Топология многообразий
6. Основные этапы развития топологии
|
Так же Вы можете узнать о... Алкана, алканна (Alkanna), род многолетних, большей частью жестковолосистых травянистых растений семейства бурачниковых. Аутентичный текст (от греч. authentikos — подлинный), текст какого-либо документа, соответствующий по содержанию тексту на другом языке и имеющий одинаковую с ним силу. Бикбай Баязит Гаязитович [9(22).1.1909, деревня Калтай, ныне Кумертаукского района, — 2. Вал отбора мощности (ВОМ), механизм силовой передачи, при помощи которого часть мощности двигателя трактора, самоходного шасси, автомобиля специального назначения и др. Волынская возвышенность, на З. УССР, между рр. Гётце Альбрехт Гётце (Goetze) Альбрехт (р. 11.1.1897), Лейпциг хеттолог и ассириолог. Гхассульская культура, археологическая культура эпохи энеолита (конец 5—4-е тыс. Домра, домра, русский щипковый струнный музыкальный инструмент. Земная станция, станция космической службы, расположенная либо на земной поверхности, включая борт морского судна, либо на борту воздушного корабля (по определению, принятому Чрезвычайной административной конференцией радиосвязи, Женева, 1963). Кабельное судно, судно для прокладки подводных (морских, океанских) кабельных линий связи (преимущественно) и электропередачи, а также для подъёма кабелей со дна и их ремонта. Кёниг Рене Кёниг (Konig) Рене (р. 5.7.1906, Магдебург), немецкий социолог (ФРГ). |
|