Теплопроводности уравнение
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ТЕА |
| ТЕБ |
| ТЕВ |
| ТЕГ |
| ТЕД |
| ТЕЖ |
| ТЕЗ |
| ТЕИ |
| ТЕЙ |
| ТЕК |
| ТЕЛ |
| ТЕМ |
| ТЕН |
| ТЕО |
| ТЕП |
| ТЕР |
| ТЕС |
| ТЕТ |
| ТЕУ |
| ТЕФ |
| ТЕХ |
| ТЕЧ |
| ТЕШ |
| ТЕЯ |
Теплопроводности уравнение,дифференциальное уравнение с частными производными параболического типа, описывающее процесс распространения теплоты в сплошной среде (газе, жидкости или твёрдом теле); основное уравнение математической теории теплопроводности. Теплопроводности уравнение выражает тепловой баланс для малого элемента объёма среды с учётом поступления теплоты от источников и тепловых потерь через поверхность элементарного объёма вследствие теплопроводности. Для изотропной неоднородной среды Теплопроводности уравнение имеет вид:
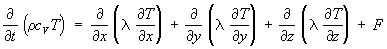 ,
,
где r — плотность среды; cv — теплоёмкость среды при постоянном объёме; t — время; х, у, z — координаты; Т = Т (х, у, z, t) — температура, которая вычисляется при помощи Теплопроводности уравнение; l — коэффициент теплопроводности; F = F (x, y, z, t) — заданная плотность тепловых источников. Величины r, Cv,l зависят от координат и, вообще говоря, от температуры. Для анизотропной среды Теплопроводности уравнение вместо l содержит тензор теплопроводности lir, где i, k = 1, 2, 3.
В случае изотропной однородной среды Теплопроводности уравнение принимает вид:
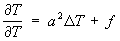 ,
,
где DT — Лапласа оператор, a2 = l/(rcv) — коэффициент температуропроводности; f = F/(rcv). В стационарном состоянии, когда температура не меняется со временем, Теплопроводности уравнение переходит в Пуассона уравнениеDТ = f/a2 = F/l или, при отсутствии источников теплоты, в Лапласа уравнениеDТ = 0. Основными задачами для Теплопроводности уравнение является Коши задача и смешанная краевая задача (см. Краевые задачи).
Первые исследования Теплопроводности уравнение принадлежат Ж. Фурье (1822) и С. Пуассону (1835). Важные результаты в исследовании Теплопроводности уравнение были получены И. Г. Петровским, А. Н. Тихоновым, С. Л. Соболевым.
Лит.: Карслоу Г. С., Теория теплопроводности, пер. с англ., М.— Л., 1947: Владимиров В. С., Уравнения математической физики, М., 1967; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.
Д. Н. Зубарев.
|
Так же Вы можете узнать о... Пржевальский Николай Михайлович [31.3(12.4). Расширяющийся цемент, собирательное название группы цементов, обладающих способностью увеличиваться в объёме в процессе твердения. Савмак (греч. Saumakos), вождь боспорских скифов, восставших в 107 до н. Си-Ся, государство, созданное в конце 10 в. тибето-бирманскими племенами минья (тангуты) на части территории современного Северо-Западного Китая и просуществовавшее до начала 13 в. Социалистические обязательства, индивидуальные или коллективные обязательства участников социалистического соревнования в социалистических странах по выполнению и перевыполнению государственных планов развития народного хозяйства, культурного строительства, повышения благосостояния трудящихся. Схоластика (лат. scholastica, от греч. scholastikos — школьный, учёный, schol Униформизм, научная концепция в геологии, исходящая из представления о неизменяемости системы геологических факторов во времени. Фототипия (от фото... и греч. typos – отпечаток, форма), способ безрастровой плоской печати иллюстраций, основанный на изменении физико-химических свойств светочувствительного слоя. Цевница, русский многоствольный духовой музыкальный инструмент типа флейты Пана. Шведов Федор Никифорович (14.2.1840—12.12.1905, Одесса), русский физико-химик. |
|